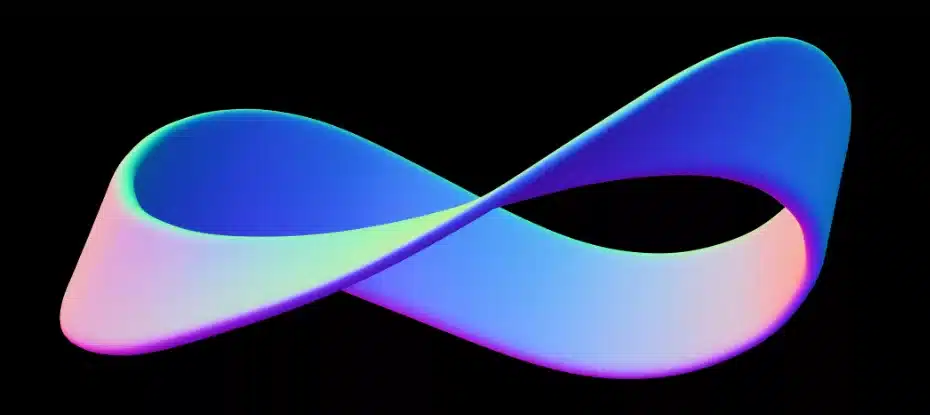Durante quase cinquenta anos, os matemáticos ficaram intrigados com uma questão aparentemente simples: quão pequena é possível fazer uma tira de Möbius sem que ela se cruze?
Agora, Richard Schwartz, um matemático da Universidade Brown, propôs uma solução elegante para este problema, que foi originalmente colocada pelos matemáticos Charles Weaver e Benjamin Halpern em 1977.
No seu artigo, Halpern e Weaver estabelecem um limite para as tiras de Möbius com base na geometria familiar dos pedaços dobrados de papel sólido – que a relação entre o comprimento e a largura do papel deve ser superior a √3, ou cerca de 1,73.
Por exemplo, uma tira de Möbius com um centímetro de comprimento precisaria ser mais larga que √3 ou 1,73 centímetros.
Schwartz diz que ficou “viciado” no problema da tira de Möbius depois de saber dele há quatro anos, durante uma conversa com um colega.
Ele teve várias tentativas de resolvê-lo ao longo dos anos e publicou um artigo em 2021 com uma abordagem promissora que acabou falhando.
Schwartz não podia deixar o problema de lado e recentemente começou a fazer experiências com tiras de papel de Möbius, na esperança de que a forma 2D fosse mais fácil de resolver matematicamente.
Mas quando ele abriu um desses loops em ângulo (o que era necessário para resolver seu problema de otimização), ele viu algo que não esperava.

O comprimento do papel 2D não parecia um paralelogramo, como ele relatou em seu primeiro artigo. Em vez disso, era um trapézio – uma forma com quatro lados retos, onde apenas dois dos lados são paralelos um ao outro .
“Vergonhosamente, descobri recentemente que cometi um erro ao configurar o problema de otimização”, escreve Schwartz .
Ao longo de três noites sem dormir – e com a ajuda de alguns colegas – Schwartz corrigiu seu erro e encontrou “uma prova muito boa” para a etapa intermediária “que simplificou bastante” o artigo.
“Fiquei surpreso e encantado ao descobrir que, quando resolvi o problema de otimização corretamente, acertei… √3 na mosca!” ele escreve.
As tiras de Möbius têm muitas propriedades estranhas, o que as tornou objetos de fascínio desde que foram descritas em 1858 pelos matemáticos alemães August Möbius e Johann Listing.
As tiras de Möbius não são orientáveis . Isto significa que uma formiga vagando em torno de uma faixa de Möbius nunca está verdadeiramente “dentro” ou “fora” ou “superior” ou “inferior” da forma.

Em suas viagens, as formigas cobrem os dois lados da fita em um movimento contínuo.
Essa capacidade de usar ambos os lados de uma superfície sem a necessidade de virar a fita tornou as tiras Möbius úteis para gravadores, máquinas de escrever, correias transportadoras, cartuchos de impressão e montanhas-russas.
Traduzido por Mateus Lynniker de ScienceAlert