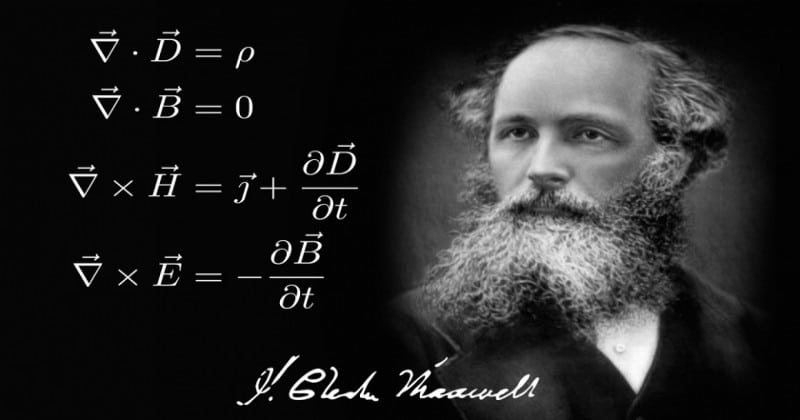Por Rishabh Nakra
Publicado no The Secrets Of The Universe
Hoje, a principal equação da física é a equivalência de energia e massa, a E = mc². Essa equação é tão famosa que até mesmo um leigo a encontrou ou a viu em algum lugar pelo menos uma vez na vida. A equivalência da energia e massa pertence à teoria da relatividade especial, idealizada por Albert Einstein em 1905. Mas qual é a origem da relatividade especial? A resposta é eletricidade e magnetismo. Sim! Você leu certo. As raízes da teoria da relatividade estão incorporadas nas quatro famosas equações da eletricidade e magnetismo, as Equações de Maxwell.
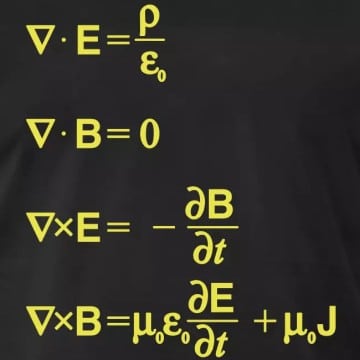
James Maxwell era um físico teórico que provou que Faraday estava certo. Faraday supôs que a luz é uma onda eletromagnética. Faraday não era um cientista teórico rigoroso, mas Maxwell era. Estas 4 equações não são formuladas por Maxwell. As duas primeiras equações são as leis de Gauss da eletricidade e do magnetismo respectivamente, a terceira equação é a lei de Faraday e a quarta é a lei circuita de Ampere com um termo de correção que foi introduzido por Maxwell. Então, por que elas são nomeadas em sua homenagem? A razão é que Maxwell reuniu essas equações independentes da eletricidade e do magnetismo e mostrou que ambos estão profundamente conectados.
As equações de Maxwell foram o ponto de virada na história da humanidade. Como Carl Sagan disse: “Elas tiveram um impacto maior na história humana do que quaisquer dez presidentes”. Vamos agora olhar para estas equações que mudam o jogo e o que elas realmente significam.
1. Lei de Gauss da Eletrostática
Significado da equação
A lei de Gauss da eletrostática nos diz três coisas importantes. Primeiro: pode existir uma carga elétrica independente no espaço. Isso significa que uma única carga positiva ou uma única carga negativa podem ter sua própria existência. Elas não precisam existir em pares. Segundo: O número de linhas de campo elétrico que sai de um volume é diretamente proporcional à carga contida nele. Terceiro: O campo elétrico, como o campo gravitacional, segue a lei do inverso do quadrado. Assim, a lei de Gauss é apenas outra versão da lei de Coulomb em eletrostática.
2. Lei de Gauss da magnetostática
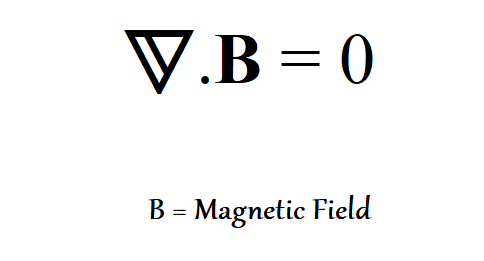
Significado da Equação
Esta é a mais fácil das quatro equações de Maxwell. O significado desta equação é: monopolos magnéticos não existem na natureza. Então, se você cortar um ímã em duas partes, não terá polos norte e sul separados. Em vez disso, você terá dois novos ímãs de barra, cada um com seu próprio par de polos norte e sul. Se monopolos magnéticos forem descobertos, o lado direito da equação mudará.
3. Lei de Faraday
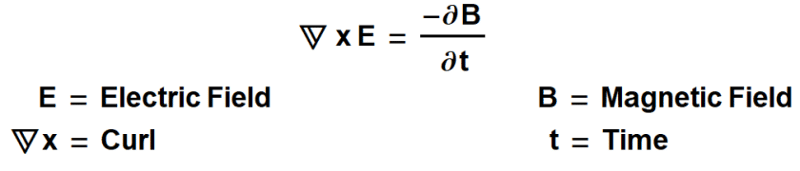
Significado da Equação
Se você estiver usando qualquer coisa que funcione com eletricidade, agradeça esta equação. Nada teria sido possível sem essa terceira equação, conhecida como a lei de Faraday. Essa equação é o arquiteto do mundo moderno. Diz, Um fluxo magnético em mudança através de um circuito fechado produzirá uma força eletromotriz nesse circuito. Uma declaração notável em si. Assim, você pode produzir um campo elétrico a partir do próprio ímã. Nenhuma outra equação capta o belo elo entre os dois campos diversos do que este. A equação de Faraday possibilitou a construção de solenoides, motores elétricos, geradores e transformadores.
4. Lei Circuita de Ampere
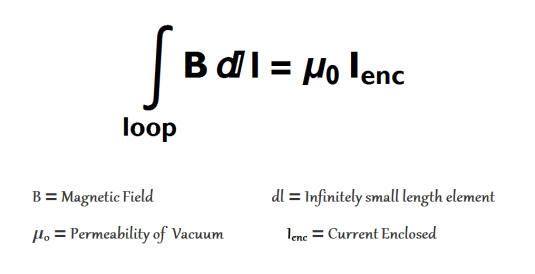
Significado da Equação
A lei de Ampere nos diz que um fio condutor atual produz um campo magnético que circunda o fio e é proporcional à quantidade de corrente que flui através do fio condutor. Bem, essa equação era um marco em si. Diz que todos os efeitos magnéticos são realmente causados pelas correntes, que nada mais são que partículas carregadas em movimento.
Outra coisa importante sobre esta lei é que ela é matematicamente incorreta na forma dada acima. Isso foi notado por Maxwell e ele acrescentou um novo termo à lei. Então a lei modificada de Ampere é:
O segundo termo do lado direito é a correção adicionada. Isso não apenas corrige a matemática da equação, mas também adiciona uma bela simetria às equações de Maxwell. A correção na verdade significa que podemos ter um campo magnético de um campo elétrico variável, exatamente oposto à terceira equação, que diz que o campo elétrico pode ser gerado a partir de um campo magnético variável.
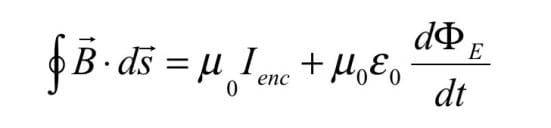
Então, agora você pode ver como essas equações são importantes para física. Essas 4 equações, juntamente com a equação da continuidade, são os blocos de construção de toda a eletrodinâmica.
Tradução fornecida por Elton Wade a partir de seu projeto de divulgação científica.
