Por Riis Rhavia Assis Bachega
Quando Richard Price publicou em 1763 a obra póstuma do reverendo Thomas Bayes (1701? – 1761) intitulada “An essay towards solving a problem in the doctrine of chances” (Tentativa de elucidar um problema na doutrina do acaso), talvez nunca imaginasse o impacto que esse trabalho teria mais de 200 anos depois. Hoje, os métodos baseados na Teoria Bayesiana das probabilidades estão sendo empregados em diversas áreas como a econometria, a bioestatística, a análise de riscos, e na minha área de atuação, a astrofísica e a cosmologia.
A teoria Bayesiana foi desenvolvida tendo em mente que nosso conhecimento sobre o mundo é imperfeito e os dados que coletamos estão impregnados de ruído, o que pode nos levar a conclusões errôneas. O primeiro a empregar o método bayesiano em problemas de física foi o matemático francês Pierre de Simon Laplace. Laplace é conhecido pelo demônio de Laplace, a ideia de que se um intelecto tivesse o conhecimento exato do estado de movimento de cada partícula no universo em um dado instante, ele poderia conhecer todos os estados passados e futuros de cada partícula. É estranho pensar que alguém como Laplace, que tinha profunda crença no num universo governado por leis determinísticas, empregasse métodos baseados em probabilidades. No entanto, Laplace estava perfeitamente ciente das imperfeições do conhecimento humano, e entendia a importância das probabilidades. Dessa forma, Laplace desenvolveu métodos para medir as órbitas e massas de Júpiter e Saturno, a despeito da imprecisão dos instrumentos da época.
Apesar do pioneirismo, a abordagem bayesiana caiu em esquecimento nas ciências, sendo preterida pela abordagem frequentista ou fisheriana em alusão ao estatístico e biólogo inglês Ronald Aylmer Fischer. Esta abordagem ainda é hegemônica, mas graças ao grande aumento na capacidade de processamento dos computadores, a abordagem bayesiana tem renascido com grande força. O objetivo desse texto é explicar os dois conceitos sobre probabilidades (frequentista e bayesiano), falar um pouco sobre o teorema de Bayes, e falar sobre as implicações mais profundas da abordagem bayesiana (ou bayesianismo) na forma como sustentamos nossas crenças e entendemos o próprio método científico.
O que é probabilidade?
- Probabilidade como frequência
O conceito clássico de probabilidade diz que probabilidade é “o número de vezes que um evento ocorre sobre o número de tentativas, no limite de uma série infinita de repetições equiprováveis”. Esse é o conceito empregado pela escola frequentista, que, no entanto, é falho por certos problemas:
- Essa definição de probabilidade é circular, pois quando definimos probabilidade em termos de frequência, assumimos que todas as repetições possuem a mesma probabilidade!
- Ela não pode ser aplicada a situações que não podem ser repetidas. Dessa maneira, não faz sentido se perguntar qual a probabilidade de os dinossauros terem sido extintos pelo impacto de um meteoro no final do mesozoico, pois esse foi um evento histórico único.
- Ele assume um limite de repetições infinitas, o que não existe na prática. Como podemos saber se o número de medidas que realizamos foi realmente suficiente? Como podemos saber se a nossa amostra é satisfatória ou não?
Outro problema do conceito frequentista está no que entendemos por aleatoriedade. Pegue o exemplo clássico de uma moeda, que ao ser jogada para cima, possui probabilidade igual a 0.5 de sair cara ou coroa ao atingir o chão. O estranho dessa frase está na palavra possui, pois parece que está conferindo a probabilidade de igual a 0.5 como uma propriedade ontológica da moeda. Porém, se tivéssemos um conhecimento detalhado da estrutura interna da moeda, assim como o conhecimento preciso das condições iniciais em que a moeda foi atirada para cima, poderíamos saber com certeza se ao cair no chão, iria sair cara ou coroa. Logo, a aparente aleatoriedade da queda da moeda se deve apenas ao nosso estado de conhecimento sobre as condições do sistema. Se insistirmos no conceito de probabilidade em termos de uma sequencia de eventos aleatórios, recairemos de novo no problema da circularidade. Para o caso da moeda, por exemplo:
“uma moeda aleatória (não viciada) é aquela em que a sequencia de caras e coroas é compatível com a hipótese de que a probabilidade de sair cara e coroa é igual a 0.5.”
Devido a esses problemas de circularidade, precisamos introduzir um novo conceito de probabilidade.
- Probabilidade como grau de crença
Muitos dos problemas referidos ao conceito clássico de probabilidade podem ser resolvidos pela abordagem bayesiana, que entende que “probabilidade é uma medida do quanto acreditamos em uma dada proposição”. Essa definição pode ser aplicada tanto a eventos que podem ser repetidos, como a acontecimentos únicos (qual a probabilidade de chover amanhã?).
Uma diferença marcante das escolas frequentista e bayesiana está em como se entende incerteza. Para os frequentista, incerteza está associada à imprecisão dos nossos instrumentos de medida (incerteza estatística) e a flutuações aleatórias daquilo que queremos medir (incerteza sistemática). Para a escola bayesiana, esses dois tipos de incerteza são indistinguíveis, existe apenas a incerteza relacionada ao nosso desconhecimento. No caso do exemplo da moeda, a aleatoriedade se deve apenas ao fato que desconhecemos as condições exatas do sistema.
Outra diferença marcante está no fato de que a abordagem bayesiana leva em conta as informações a priori que temos sobre o mundo. Por exemplo, se vamos medir a massa de um planeta extra-solar, ela tem que ser positiva, e devemos considerar isso na análise. Omitir essas expectativas pode levar a erros drásticos. Já considerar aquilo que sabemos previamente pode poupar muito trabalho.
O Teorema de Bayes
O teorema de Bayes é um resultado imediato da regra do produto de probabilidades (no entanto, pode ser deduzido de maneira muito mais rigorosa pelos axiomas lógicos de Cox). Quando temos dois eventos condicionados A e B, a probabilidade conjunta desses dois eventos ocorrerem é
o que quer dizer que a probabilidade conjunta dos eventos A e B ocorrerem é igual a probabilidade do evento B ocorrer multiplicado pela probabilidade do evento A ocorrer dado que o evento B ocorreu (e I significa qualquer informação que você tenha disponível). Se estivermos interessado somente na probabilidade do evento B ocorrer, calculamos a probabilidade marginal de B, dada por
em que somamos sobre todas as possibilidades de A. Assumindo que P(A,B|I)=P(B,A|I), podemos reescrever a regra do produto na forma do teorema de Bayes 
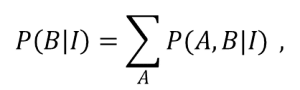
A interpretação desse teorema fica bem mais profunda se considerarmos a variável A como os dados observados D e a variável B como a hipótese H que queremos testar, obtendo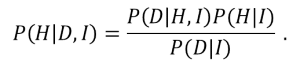
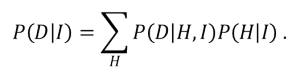
O lado esquerdo P(H|D,I) é chamado de probabilidade posterior de uma hipótese ser validada pelos dados. Ela é proporcional a distribuição de probabilidade dos dados P(D|H,I), chamada comumente de função de verossimilhança multiplicada pela probabilidade a priori P(H|I) da hipótese ser verdadeira (chamada simplesmente de prior). O prior representa o estado de conhecimento que temos antes de analisar os dados. Se somarmos sobre todas as hipóteses possíveis, a probabilidade total é igual a 1, e dessa forma podemos isolar o denominador e obter que 
Esse termo representa uma normalização e é chamado de evidência bayesiana. Ele será muito importante na parte referente à comparação de modelos. A consequência mais profunda do teorema de Bayes é que ele representa uma sequencia lógica em que saímos do prior para a posterior, em um processo de atualização de crenças, ao comparar nossas crenças prévias com os dados novos. Esse processo de atualização de crenças é chamado de inferência bayesiana ou simplesmente, regra de Bayes.
Priors e Subjetividade
A principal crítica à teoria bayesiana é que ela tem um fator que é subjetivo, a escolha do prior. Como a ciência segue um ideal de objetividade, uma abordagem que adota fatores subjetivos não seria apropriada. No entanto, reconhecer que existe a subjetividade e que todo tem crenças prévias sobre o mundo é um aspecto importante e é melhor ser explicitado do que buscar um ideal de objetividade inalcançável, sendo que o viés do cientista vai está disfarçado em uma aparente análise objetiva.
Existe um trabalho na área das ciências médicas, feito pelo pesquisador John P. Ioannidis intitulado “Why Most Published Research Findings Are False”[1] em que o autor argumenta que a maioria das hipóteses anunciadas como verdadeiras em publicações de medicina e outras áreas acadêmicas é na verdade falsa. Para se ter ideia, os laboratórios Bayer se viram incapazes de reproduzir cerca de dois terços das descobertas positivas anunciadas em publicações acadêmicas.
Encontrar falsos positivos é um problema recorrente, e será uma tendência cada vez maior com o crescimento exponencial do volume de dados, o famoso Big Data. Como argumenta Nate Silver em “O Sinal e o Ruído”, ter muitos dados e informações disponíveis não é sinônimo de ter um melhor conhecimento. Dados são inúteis se eles não estiverem contextualizados. Se não soubermos como analisa-los e interpreta-los, não iremos saber extrair informação deles e a tendência será de encontrar padrões onde eles não existem, o chamado overfitting. Em resumo, temos que aprender a separar o sinal do ruído.
O princípio básico da inferência bayesiana é que não há como haver inferência sem assumirmos certas crenças prévias. E longe de destruir a objetividade, é possível mostrar que quanto mais dados e quão mais precisos eles forem, a escolha do prior tende a fazer menos diferença no cálculo da posterior. Também temos que lembrar que se dois cientistas possuem o mesmo estado de conhecimento, eles tenderão a escolher o mesmo prior, e dessa forma obter a mesma posterior se analisarem os mesmos dados.
Um caso de falso positivo
Um exemplo muito utilizado para exemplificar a aplicação do teorema de Bayes e como ele pode prevenir falsos positivos é dado pelo pesquisador em inteligência artificial, Eliezer Yudkowski[2]. Se trata de um exemplo com mamografias. Recomendam-se que a partir dos 40 anos que mulheres façam mamografias anualmente. Nessa idade, cerca de 1% das mulheres são portadoras de um tumor assintomático de mama. Sabe-se que a mamografia apresenta resultado positivo em 80 % das mulheres com câncer de mama, mas que esse resultado ocorre em 9,6% das mulheres sem o câncer.
Se uma mulher jovem fizer uma mamografia e o resultado der positivo, qual a probabilidade de ela realmente ter câncer? Consideremos a hipótese dela ter câncer como H1 e a hipótese dela não ter câncer como H2. O prior para a primeira hipótese é P(H1|I)=0,01, e o para a segunda hipótese é P(H2|I)=0,99. Como sabemos que 80% das mamografias dão resultado positivo quando a mulher tem câncer de mama, então a verossimilhança será P(D|H1,I)=0,8. Também sabemos que o percentual de falsos positivos é P(D|H2,I)=0,096. Aplicando o teorema de Bayes, temos que a probabilidade dela ter câncer é P(H1|D,I)=0,8×0,01/(0,8×0,01+0,096×0,99)=0,077. Ou seja, a probabilidade de o exame ter dado um falso positivo é de mais de 90%, e a mulher pode ficar mais tranquila. Esse é um ótimo exemplo de como temos que levar em conta o contexto e todas as informações prévias para evitarmos falsos positivos.
Evidência Bayesiana e a Navalha de Occam
O teorema de Bayes fornece um método de comparar diferentes modelos teóricos, além de formular quantitativamente o princípio da navalha de Occam[3] – a teoria mais simples compatível com as evidências disponíveis deve ser a preferida. Não devemos introduzir hipóteses adicionais se as que temos disponíveis explicam bem os fenômenos. Para modelos teóricos, consideramos um espaço contínuo de parâmetros θ fazendo o papel das nossas hipóteses a serem validadas e o modelo M a ser considerado. Dessa forma, a expressão para a evidência é dada pela integral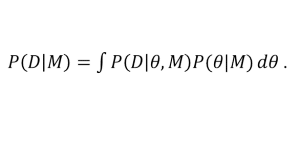
Um bom modelo é aquele que fita os dados disponíveis e faz boas previsões. Quanto mais parâmetros o modelo tiver, melhor ele vai fitar os dados. Comparar modelos significa tirar a razão entre as evidências de diferentes modelos, sendo que o modelo que tiver mais parâmetros será penalizado.
Epistemologia Bayesiana
A adoção dos métodos bayesianos está promovendo uma revolução na ciência, não só pelos métodos estatísticos de análise de dados e processamento de informação, mas a ponto de redefinir a ciência em si. O próprio método científico apresenta ter uma lógica e estrutura bayesiana, uma vez que ele consiste em elaborar hipóteses, testá-las com experiências e observações e reajustar as nossas crenças iniciais de acordo com as evidências, ou seja, todo o processo de inferência descrito pelo teorema de Bayes.
Outra coisa importante a se destacar é o critério bayesiano de seleção de modelos/teorias. Quando comparamos dois modelos diferentes, calculamos a evidência para cada modelo e depois tiramos a razão entre elas. Seguindo critérios prescritos pela escala de Jeffrey, podemos dizer qual modelo os dados preferem e com qual intensidade.
O critério bayesiano não nos diz se um modelo é verdadeiro ou falso, ele diz qual possui maior plausibilidade, em qual deles podemos ter maior confiança. Também, é inútil tentar descobrir se uma hipótese é verdadeira ou falsa por si mesma, você tem que ter uma hipótese alternativa para comparar com a sua hipótese original e descobrir qual é a mais plausível.
Esse critério é bem mais amplo que o restrito critério de falseabilidade defendido por Karl Popper, por que não é baseado no “tudo-ou-nada”. Na realidade da prática científica, nenhum resultado experimental, por mais preciso, pode falsear definitivamente uma hipótese, apenas aumentar ou diminuir sua credibilidade, se comparada com outras hipóteses disponíveis. Dada toda a complexidade da ciência contemporânea, com um imenso volume de dados, mas também uma maior dificuldade de processá-los e interpretá-los, o critério da falseabilidade está, podemos dizer defasado, e o critério bayesiano se mostra muito mais adequado.
Outra coisa que vale mencionar é a ligação da regra de Bayes com o processo de aprendizagem, tanto de pessoas quanto de máquinas. Tanto que existe toda uma categoria de algoritmos computacionais, conhecidos como algoritmos de machine learning baseado em critérios bayesianos.
Conclusão
A regra de Bayes, muito além de um resultado matemático útil, dá origem a toda uma visão de mundo e quantifica o que é ser racional. A expressão matemática do teorema de Bayes liga a inferência racional (probabilidade posterior) com a subjetividade das nossas visões prévias (prior) e as evidências empíricas (função de verossimilhança). Outra coisa a se destacar é que o teorema de Bayes computa também a irracionalidade, pois se temos total certeza na validade ou falsidade de uma proposição (o que significa um prior igual a 100% e 0% respectivamente), não importa todas as evidências empíricas vindouras, continuaremos tendo certeza absoluta na veracidade ou falsidade de uma proposição. Para podermos mudar nossas crenças, não podemos ter crenças prévias absolutas. Se considerarmos uma proposição bastante implausível (como a existência de alienígenas nos visitando), teremos um prior próximo de zero, o que significa que para mudar nossa crença prévia, precisaremos ter evidências muito contundentes, quantificando a frase de Carl Sagan de que “grandes alegações exigem grandes evidências”. Como bem dito por Eliezer Yudkowski, o teorema de Bayes liga a razão humana ao universo físico.
Referências Bibliográficas
PENA, Sérgio Danilo; “Thomas Bayes: o ‘cara’!”. Ciência Hoje, vol. 38, nº 228 (2006);
SILVER, Nate; “O Sinal e o Ruído”. Ed. Intrínseca, (2013);
TROTTA, Roberto; “Bayes in the sky: Bayesian inference and model selection in cosmology”. Contemporary Physics, vol. 49, nº 2 (2008).
DOI: http://dx.doi.org/10.1080/00107510802066753;
Toussaint, Udo Von; “Bayesian inference in physics”. Review of modern physics, vol. 83 (2011).
[1] IOANNIDIS, John P.A. “Why Most Published Research Findings Are False”. PLOS Medicine, 2, e124, agosto de 2005.
[2] “Na Intuitive explanation fo bayesian reasoning” ( Yudkowsky, 2003, em youdkowsky.net/bayes/bayes.html).
[3] Em alusão ao frade franciscano e lógico inglês Guilherme de Occam (1285-1347).
