Tornando simples o emaranhamento quântico

Por Frank Wilczek
Publicado na Quanta Magazine

Uma aura de glamour misterioso é atribuído ao conceito de entrelaçamento quântico, e também na reivindicação relacionada (de alguma forma) que a teoria quântica exige “muitos mundos”. Mas afinal, aquelas que são, ou devem ser, ideias científicas, devem ter sentidos verdadeiros e implicações concretas. Aqui eu gostaria de explicar que os conceitos de emaranhamento e muitos mundos são tão simples e claros quanto eu saiba.

I.

Emaranhamento é frequentemente considerado como um fenômeno exclusivamente da mecânica quântica, mas não é. Na verdade, é esclarecedor, embora um pouco não-convencional, considerar uma versão simples não-quântica (ou “clássica”) de emaranhamento, em primeiro lugar. Isso nos permite erguer a sutileza do próprio emaranhamento além da estranheza geral da teoria quântica.

O emaranhamento surge nas situações em que temos conhecimento parcial do estado de dois sistemas. Por exemplo, os nossos sistemas podem ser dois objetos que vamos chamá-los de ‘C-ons’. Pretendo sugerir “C” como “clássico”, mas se você preferir ter algo específico e agradável em mente, você pode pensar em nossos C-ons como bolos.

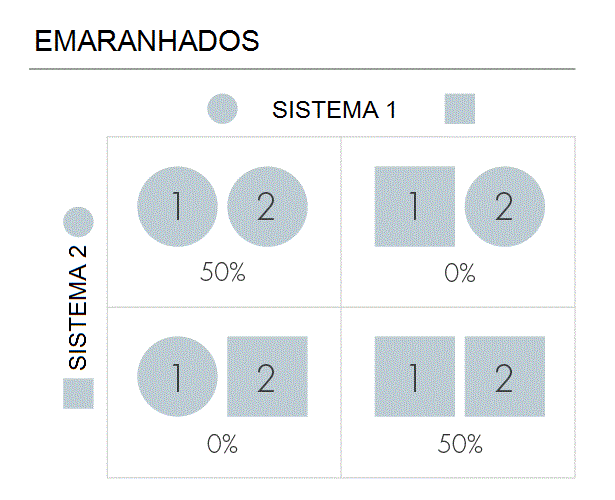
Nossos C-ons vêm de duas formas, quadrados ou circulares, que identificamos como seus possíveis estados. Em seguida, os quatro estados que tem possíveis conjuntos, por dois C-ons, são (quadrado, quadrado), (quadrado, círculo), (círculo, quadrado), (círculo, círculo). As tabelas a seguir mostram dois exemplos de quais probabilidades poderiam ser para encontrar o sistema em cada um desses quatro estados.

Dizemos que os C-ons são “independentes” se o conhecimento do estado de um deles não der informações úteis sobre o estado do outro. Nossa primeira tabela tem esta propriedade. Se o primeiro C-on (ou bolo) for quadrado, ainda estaremos ignorantes sobre a forma do segundo. Da mesma forma, a forma do segundo não revela nada útil sobre a forma do primeiro.

Por outro lado, dizemos que nossos dois C-ons estão emaranhados quando as informações sobre um melhora nosso conhecimento sobre o outro. Nossa segunda tabela demonstra um emaranhamento extremo. Neste caso, sempre que o primeiro C-on for circular, sabemos que o segundo é circular também. E quando o primeiro C-on for quadrado, então o segundo também será. Sabendo a forma de um, podemos inferir a forma do outro, com certeza.

A versão quântica do emaranhamento tem essencialmente o mesmo fenômeno – ou seja, a falta de independência. Na teoria quântica, os estados são descritos por objetos matemáticos chamados de funções de onda. As regras de ligação das funções de onda de probabilidades físicas apresentam complicações muito interessantes, como veremos, mas o conceito central do conhecimento do emaranhado, que já vimos nas probabilidades clássicas, nos levará melhor [nesse caminho].

Bolos não contam como sistemas quânticos, é claro, mas o emaranhamento entre sistemas quânticos surge naturalmente – por exemplo, na sequência de colisões de partículas. Na prática, estados não-emaranhados (independentes) são raras exceções, pois sistemas sempre interagem. A interação cria correlações entre eles.

Considere, por exemplo, moléculas. Elas são compostas de subsistemas, nomeadamente elétrons e núcleos. O estado de menor energia de uma molécula, em que é mais usualmente encontrado, é um estado altamente emaranhado dos seus elétrons e núcleos, para as posições das referidas partículas constituintes não estarem de forma independente. Com os núcleos se movendo, os elétrons movem-se com eles.

Voltando ao nosso exemplo: Se escrevermos Φ■, Φ● para as funções do sistema de onda 1 descrito em seus estados quadrados ou circulares, e ψ■, ψ● para as funções de onda do sistema 2 descrito em seus estados quadradas ou circulares, em seguida, em nosso exemplo de trabalho, os estados gerais serão

• Independentes: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●
• Emaranhados: Φ■ ψ■ + Φ● ψ●

Nós também podemos escrever a versão independente como

(Φ■ + Φ●) (ψ■ + ψ●)

Note como, nesta formulação entre parênteses, sistemas são claramente separados em 1 e 2 em unidades independentes.

Há muitas maneiras de criar estados emaranhados. Uma maneira é fazer uma medição do seu sistema (composto) que lhe dará informações parciais. Nós podemos saber, por exemplo, que os dois sistemas conspiraram para ter a mesma forma, sem aprender exatamente qual forma eles têm. Este conceito se tornará importante mais tarde.

As consequências mais distintivas do entrelaçamento quântico, tais como os efeitos de Einstein-Podolsky-Rosen (EPR) e Greenberger-Horne-Zeilinger (GHZ), surgem através de sua interação com outro aspecto da teoria quântica chamado de “complementaridade”. Para abrir caminho para a discussão do EPR e GHZ, deixe-me agora apresentar a complementaridade.

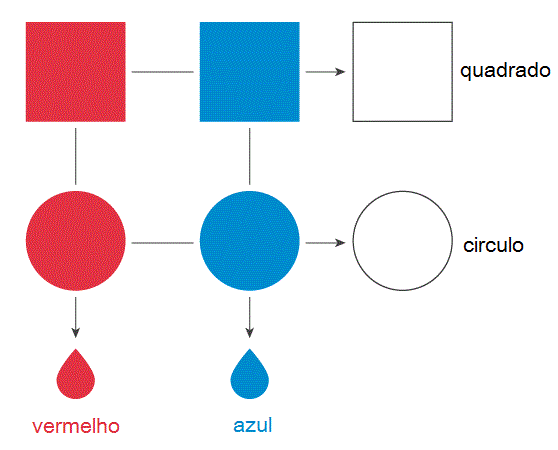
Anteriormente, nós imaginamos que nossos C-ons poderiam exibir duas formas (quadrado e círculo). Agora vamos imaginar que ele também pode apresentar duas cores – vermelho e azul. Se estivéssemos falando de sistemas clássicos, como bolos, esta propriedade acrescentada implicaria que nossos C-ons poderiam estar em qualquer um dos quatro estados possíveis: quadrado vermelho, círculo vermelho, quadrado azul ou círculo azul.

No entanto, para um bolo quântico – um terremoto*, talvez, ou (com mais dignidade) uma Q-on – a situação é profundamente diferente. O fato de uma Q-on poder apresentar, em diferentes situações, diferentes formas ou diferentes cores não significa necessariamente que ela possui tanto uma forma quanto uma cor, simultaneamente. Na verdade, esse “senso comum” de inferência, que Einstein insistiu que deve ser parte de qualquer noção aceitável da realidade física, é inconsistente com os fatos experimentais, como veremos em breve.

*[N.T.: Trocadilho inglês da palavra Cake (bolo) com a palavra Quake (terremoto)]

Podemos medir a forma de nosso Q-on, mas ao fazê-lo, perdemos todas as informações sobre sua cor. Ou podemos medir a cor de nosso Q-on, mas ao fazê-lo, perdemos todas as informações sobre a sua forma. O que não podemos fazer, de acordo com a teoria quântica, é medir a sua forma e cor ao mesmo tempo. Nenhuma visão da realidade física capta todos os seus aspectos; é preciso levar em conta muitos pontos de vista diferentes, mutuamente exclusivos, cada um oferecendo uma visão válida, mas parcial. Este é o coração da complementaridade, como Niels Bohr formulou.

Como consequência, as forças da teoria quântica são cautelosas em atribuir propriedades invididuais à realidade física. Para evitar contradições, temos de admitir que:

1. Uma propriedade que não é medida não precisa existir.
2. A medição é um processo ativo modifica o sistema que está sendo medido.

II.

Agora vou descrever duas ilustrações clássicas – embora estejam longe de ser clássicas! – de estranhezas da teoria quântica. Ambos foram verificados em experimentos rigorosos. (Nas experiências reais, as pessoas mediram as propriedades com o momento angular dos elétrons em vez de formas ou cores de bolos).

Albert Einstein, Boris Podolsky e Nathan Rosen (EPR) descreveram um efeito surpreendente que pode surgir quando dois sistemas quânticos estão entrelaçados. O efeito EPR se casa com uma forma específica, experimentalmente realizada, do emaranhamento quântico com a complementaridade.

Um par de EPRs consiste em dois Q-ons, cada um dos quais podem ser medidos quer pela sua forma, quer pela sua cor (mas não para ambos). Assumimos que temos acesso a muitos desses pares, todos idênticos, e que podemos escolher quais as medidas de garantir seus componentes. Se medirmos a forma de um membro de um par de EPR, achamos que é igualmente suscetível ser quadrado ou circular. Se medirmos a cor, achamos que tem a mesma probabilidade de ser vermelho ou azul.

Os efeitos interessantes, que o EPR considerou paradoxal, surgem quando fazemos medições de ambos os membros do par. Quando medimos os dois membros para a cor, ou ambos os membros de forma, descobrimos que os resultados sempre coincidem. Assim, se acharmos que um é vermelho, e depois medirmos a cor do outro, vamos descobrir que ele também é vermelho, e assim por diante. Por outro lado, se medirmos a forma de um, e, em seguida, a cor de outro, não existe uma correlação. Assim, se o primeiro é quadrado, o segundo tem a mesma probabilidade de ser vermelho ou azul.

Vamos, de acordo com a teoria quântica, obter esses resultados, mesmo a grandes distâncias, separando os dois sistemas, e as medições sendo realizadas quase que simultaneamente. A escolha de uma medição em um local parece estar afetando o estado do sistema no outro local. Esta “ação fantasmagórica à distância”, como Einstein o chamou, pode parecer exigir a transmissão de informações – neste caso, as informações sobre o que a medição foi realizada – a uma taxa mais rápida do que a velocidade da luz.

Mas não é assim? Até eu souber sobre o resultado obtido, eu não saberei o que esperar. Eu obterei informações úteis quando eu aprender o resultado que você mediu, e não no momento em que medi-lo. E qualquer mensagem revelando o resultado medido deve ser transmitida, de alguma forma física concreta, porém (presumivelmente) mais lenta do que a velocidade da luz.

Após uma reflexão mais profunda, o paradoxo se dissolve mais. Com efeito, vamos considerar de novo o estado do segundo sistema, dado que o primeiro foi medido como sendo vermelho. Se nós escolhemos medir a cor do segundo Q-on, certamente irá ficar vermelho. Mas, como discutimos anteriormente, diluindo a introdução de complementaridade, se nós escolhermos medir a forma de um Q-on, quando se está no estado “vermelho”, teremos igual probabilidade de encontrar um quadrado ou um círculo. Assim, longe de introduzir um paradoxo, o resultado do EPR é logicamente forçado. Ele está, em essência, simplesmente reembalando a complementaridade.

Também não é paradoxal descobrir que eventos distantes estão correlacionados. Afinal, se eu colocar cada membro de um par de luvas em caixas e enviá-los para os lados opostos da Terra, eu não deveria me surpreender ao olhar dentro de uma caixa que pode determinar a lateralidade da outra. Da mesma forma, em todos os casos conhecidos, as correlações entre um par de EPRs devem ser impressos quando os seus membros estão juntos, embora, naturalmente, eles possam sobreviver a separação subsequente, como se tivessem memórias. Mais uma vez, a peculiaridade da EPR não é uma correlação como tal, mas a sua forma de realização possível em formas complementares.

III.

Daniel Greenberger, Michael Horne e Anton Zeilinger descobriram outro exemplo brilhantemente iluminante do entrelaçamento quântico. Trata-se de três dos nossos Q-ons, preparados em um estado emaranhado especial (o estado GHZ). Nós distribuímos três Q-ons para três experimentadores distantes. Cada experimentador escolhe, de forma independente e ao acaso, e devem medir a forma ou cor, e registrar o resultado. O experimento se repete muitas vezes, sempre com os três Q-ons começando no estado GHZ.

Cada pesquisador, separadamente, encontra resultados maximamente aleatórios. Quando ele mede a forma de um Q-on, ele tem a mesma probabilidade de encontrar um quadrado ou um círculo; quando ele mede a sua cor, vermelho ou azul são igualmente prováveis. Tão longe, tão mundano.

Porém, mais tarde, quando os pesquisadores se reúnem e comparam as suas medições, um pouco de análise revela um resultado impressionante. Vamos chamar as formas quadradas e cores vermelhas de “boas”, e as formas circulares e cores azuis de “más”. Os experimentadores descobrem que sempre que dois deles escolhem medir a forma, mas com uma terceira cor medida, eles descobriram que exatamente 0 ou 2 resultados eram “más” (isto é, circular ou azul). Mas quando todos os três escolhem medir a cor, eles descobrem que exatamente 1 ou 3 medições eram “más”. Isso é o que a mecânica quântica prevê, e é isso que é observado.

Então: a quantidade de mal é par ou ímpar? Ambas as possibilidades são realizadas, com certeza, em diferentes tipos de medições. Somos forçados a rejeitar a questão. Não faz sentido falar da quantidade de mal em nosso sistema, independente de como ele é medido. Com efeito, ele conduz a contradições.

O efeito GHZ é, nas palavras do físico Sidney Coleman, “A mecânica quântica em sua face”. Ele derruba um preconceito profundamente enraizado na experiência cotidiana que os sistemas físicos têm propriedades definidas, independentemente de saber se essas propriedades são medidas. Porque, se elas fossem assim, então o equilíbrio entre o bem e o mal não seria afetado por escolhas de medição. Uma vez internalizado, a mensagem do efeito GHZ é inesquecível e didático.

IV.

Até agora temos considerado como o emaranhamento pode tornar impossível atribuir únicos estados independentes para várias Q-ons. Considerações semelhantes aplicam-se a evolução de um único Q-on no tempo.

Nós dizemos que temos “histórias entrelaçadas” quando é impossível atribuir um estado definitivo para o nosso sistema em cada momento no tempo. Da mesma forma de como chegamos ao entrelaçamento convencional, eliminando algumas possibilidades, podemos criar histórias entrelaçadas fazendo medições que reúnem informações parciais sobre o que aconteceu. Nas histórias mais simples de emaranhados, temos apenas um Q-on, que nós monitoramos em dois momentos diferentes. Podemos imaginar situações em que nós determinamos qual era a forma do nosso Q-on: quadrado em ambas as vezes, ou circular ambas as vezes; mas as nossas observações deixam ambas as alternativas em jogo. Esta é uma analogia quântico-temporal das mais simples situações de emaranhamento ilustrados acima.

Usando um protocolo ligeiramente mais elaborado, podemos adicionar o enrugamento da complementaridade a este sistema, e definir situações que trazem ao aspecto dos “muitos mundos” da teoria quântica. Assim, a nossa Q-on pode ser preparada no estado vermelho em um momento anterior, e medida no estado azul em um momento posterior. Como nos exemplos simples acima, não podemos consistentemente atribuir a nossa Q-on a propriedade de cor, pois, às vezes, elas são intermediárias; nem tem uma forma determinada. Histórias desse tipo percebem, de forma limitada, mas controlada e precisa, a intuição que está na base da imagem dos muitos mundos da mecânica quântica. Um estado definitivo pode ramificar em trajetórias históricas mutuamente contraditórias, que mais tarde se reúnem.

Erwin Schrödinger, um dos fundadores da teoria quântica que era profundamente cético em relação a sua correção, enfatizou que a evolução dos sistemas quânticos naturalmente leva a estados que podem ser medidos por ter propriedades grosseiramente diferentes. Seus estados, o famoso “gato de Schrödinger”, ampliou a incerteza quântica em questões sobre a mortalidade felina. Antes da medição, como vimos em nossos exemplos, não se pode atribuir a propriedade de vida (ou morte) para o gato. Ambos – ou nenhum – coexistem dentro de um submundo de possibilidades.

A linguagem cotidiana é mal-adequada para descrever a complementaridade quântica, em parte porque a experiência cotidiana não a encontra. Gatos práticos interagem com moléculas de ar circundante, entre outras coisas, de maneiras muito diferentes, dependendo se eles estão vivos ou mortos, para que, na prática, a medição seja feita automaticamente, e o gato fique com a sua vida (ou morte). Mas histórias entrelaçadas descritas em Q-ons são, em um sentido real, gatos de Schrödinger. Sua descrição completa exige, às vezes de forma intermediária, que levemos as duas propriedades de trajetórias contraditórias em conta.

A realização experimental controlada de histórias entrelaçadas é delicada, porque exige que reunamos informações parciais sobre a nossa Q-on. Medições quânticas convencionais geralmente recolhem a informação completa de uma só vez – por exemplo, determinam uma forma definida, ou uma cor definida – em vez de uma informação parcial abrangida várias vezes. Mas isso pode ser feito, na verdade, sem grande dificuldade técnica. Desta forma, podemos dar significado matemático e experimental definitivo para a proliferação dos “muitos mundos” da teoria quântica, e demonstrar a sua substancialidade.