Por Kevin Hartnett
Publicado na Quanta Magazine
Em novembro de 1915, em uma palestra para a Academia Prussiana de Ciências, Albert Einstein descreveu uma ideia que subjugou a visão da humanidade sobre o universo. Em vez de aceitar a geometria do espaço e do tempo como fixos, Einstein explicou que habitamos uma realidade quadridimensional chamada espaço-tempo, cuja forma flutua em resposta à matéria e à energia.
Einstein elaborou essa percepção dramática em várias equações, referidas como suas “equações de campo”, que formam o núcleo de sua teoria da relatividade geral. Essa teoria foi justificada por todos os testes experimentais lançados no século passado.
No entanto, mesmo que a teoria de Einstein pareça descrever o mundo que observamos, a matemática subjacente a ele permanece em grande parte misteriosa. Os matemáticos conseguiram provar muito pouco sobre as próprias equações. Sabemos que elas funcionam, mas não podemos dizer exatamente por quê. Mesmo Einstein teve que recorrer a aproximações, em vez de soluções exatas, para ver o universo através das lentes que ele criou.
No último ano, no entanto, os matemáticos trouxeram a matemática da relatividade geral a um foco mais nítido. Dois grupos apresentaram provas relacionadas a um problema importante na relatividade geral, chamado conjectura da estabilidade do buraco negro. Seu trabalho prova que as equações de Einstein combinam com uma intuição física de como o espaço-tempo deve se comportar: se você o sacode, ele balança como gelatina, então se estabelece em uma forma estável como no início.
“Se essas soluções fossem instáveis, isso implicaria que elas não são físicas. Eles seriam um fantasma matemático que existe matematicamente e não tem significado do ponto de vista físico”, disse Sergiu Klainerman, matemático da Universidade de Princeton e co-autor, com Jérémie Szeftel, de um dos dois novos resultados.
Para completar as provas, os matemáticos tiveram que resolver uma dificuldade central nas equações de Einstein. Para descrever como a forma do espaço-tempo evolui, você precisa de um sistema de coordenadas – como linhas de latitude e longitude – que informam a localização dos pontos. E no espaço-tempo, como na Terra, é difícil encontrar um sistema de coordenadas que funcione em todos os lugares.
Agite um buraco negro
A relatividade geral é famosa por descrever o espaço-tempo como um tecido emborrachado. Sem matéria, o tecido é plano. Mas comece a jogar bolas nele – estrelas e planetas – e o tecido se deforma. As bolas rolam em direção uma da outra. E à medida que os objetos se movem, a forma do tecido de borracha muda em resposta.
As equações de campo de Einstein descrevem a evolução da forma do espaço-tempo. Você dá as informações das equações sobre curvatura e energia em cada ponto, e as equações lhe dizem a forma do espaço-tempo no futuro. Dessa forma, as equações de Einstein são como equações que modelam qualquer fenômeno físico: ali é onde a bola está no tempo zero, e ali é onde ela está cinco segundos depois.
“Eles são uma versão quantitativa matematicamente precisa da afirmação de que de que o espaço-tempo se curva na presença de matéria”, disse Peter Hintz, pesquisador da Clay na Universidade da Califórnia, em Berkeley, e coautor, com András Vasy, da Universidade de Berkeley, do outro resultado recente.
Em 1916, quase imediatamente após Einstein ter lançado sua teoria da relatividade geral, o físico alemão Karl Schwarzschild encontrou uma solução exata para as equações que descrevem o que hoje conhecemos como um buraco negro (o termo não seria inventado por outras cinco décadas). Mais tarde, os físicos encontraram soluções exatas que descrevem um buraco negro rotativo e outro com carga elétrica.
Estas permanecem as únicas soluções exatas que descrevem um buraco negro. Se você adicionar até mesmo um segundo buraco negro, a interação de forças se torna muito complicada para as técnicas matemáticas atuais lidarem com todas as situações, exceto as mais especiais.
No entanto, você ainda pode fazer perguntas importantes sobre esse grupo limitado de soluções. Uma dessas questões desenvolveu-se fora do trabalho em 1952 pelo matemático francês Yvonne Choquet-Bruhat. Ele pergunta, na verdade: o que acontece quando você agita um buraco negro?
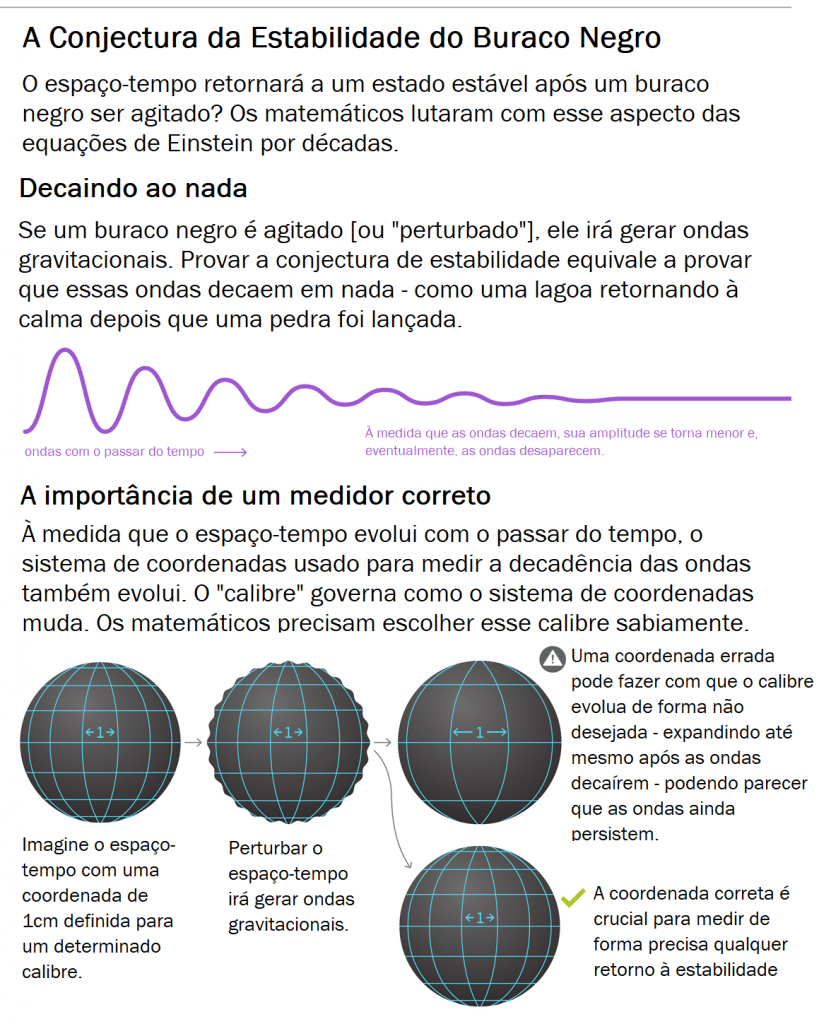
Este problema é agora conhecido como a conjectura de estabilidade do buraco negro. A conjectura prevê que as soluções para as equações de Einstein serão “estáveis sob perturbação”. Informalmente, isso significa que se você mexer em um buraco negro, o espaço-tempo vai tremer a princípio, antes de se estabelecer em uma forma que se parece muito com a forma inicial. “A grosso modo, estabilidade significa pegar soluções especiais e perturbá-las um pouco, mudar um pouco os dados e, em seguida, a dinâmica resultante será muito próxima da solução original”, disse Klainerman.
Os chamados resultados de “estabilidade” são um teste importante de qualquer teoria física. Para entender o porquê, é útil considerar um exemplo mais familiar do que um buraco negro.
Imagine uma lagoa. Agora imagine que você perturbe a lagoa atirando em uma pedra. A lagoa irá ondular um pouco e depois ficar imóvel novamente. Matematicamente, as soluções para as equações que você usa para descrever a lagoa (neste caso, as equações de Navier-Stokes) devem descrever esse quadro físico básico. Se as soluções iniciais e de longo prazo não corresponderem, você poderá questionar a validade de suas equações.
“Essa equação pode ter quaisquer propriedades, pode ser perfeitamente bem matematicamente, mas se for contra o que você espera fisicamente, não pode ser a equação correta”, disse Vasy.
Para os matemáticos que trabalham com as equações de Einstein, as provas de estabilidade têm sido ainda mais difíceis de encontrar do que soluções para as próprias equações. Considere o caso do espaço vazio e plano de Minkowski – a mais simples de todas as configurações de espaço-tempo. Essa solução para as equações de Einstein foi encontrada em 1908 no contexto da teoria anterior da relatividade especial de Einstein. No entanto, só em 1993 os matemáticos conseguiram provar que, se você mexer no espaço-tempo vazio e plano, você acaba voltando ao espaço vazio e plano. Esse resultado, por Klainerman e Demetrios Christodoulou, é um trabalho célebre no campo.
Uma das principais dificuldades com as provas de estabilidade tem a ver com acompanhar o que está acontecendo no espaço-tempo quadridimensional à medida que a solução evolui. Você precisa de um sistema de coordenadas que permita medir distâncias e identificar pontos no espaço-tempo, assim como linhas de latitude e longitude nos permitem definir locais na Terra. Mas não é fácil encontrar um sistema de coordenadas que funcione em todos os pontos no espaço-tempo e continue a funcionar à medida que a forma do espaço-tempo evolui.
“Não sabemos uma maneira única de fazer isso”, escreveu Hintz em um e-mail. “Afinal, o universo não lhe entrega um sistema de coordenadas preferido.”
O problema de medição
A primeira coisa a reconhecer sobre sistemas de coordenadas é que eles são uma invenção humana. A segunda é que nem todo sistema de coordenadas funciona para identificar cada ponto em um espaço.
Tome linhas de latitude e longitude: elas são arbitrárias. Os cartógrafos poderiam ter ungido qualquer número de linhas imaginárias com 0 graus de longitude. E enquanto a latitude e a longitude trabalham para identificar praticamente todos os locais da Terra, elas param de fazer sentido nos polos norte e sul. Se você não sabia nada sobre a própria Terra, e só tinha acesso a leituras de latitude e longitude, você poderia erroneamente concluir que há algo topologicamente estranho acontecendo nesses pontos.
Essa possibilidade – de tirar conclusões erradas sobre as propriedades do espaço físico porque o sistema de coordenadas usado para descrevê-lo é inadequado – está no centro do motivo pelo qual é difícil provar a estabilidade do espaço-tempo.
“Pode ser que a estabilidade seja verdadeira, mas você está usando coordenadas que não são estáveis e, portanto, você sente falta do fato de que a estabilidade é verdadeira”, disse Mihalis Dafermos, matemático da Universidade de Cambridge, estudioso das equações de Einstein.
No contexto da conjectura de estabilidade do buraco negro, qualquer sistema de coordenadas que você esteja usando tem que evoluir à medida que a forma do espaço-tempo evolui – como uma luva justa ajustada conforme a mão que ela envolve muda de forma. O ajuste entre o sistema de coordenadas e o espaço-tempo tem que ser bom no início e permanecer bom por toda parte. Se isso não acontecer, há duas coisas que podem acontecer para derrotar os esforços para provar a estabilidade.
Primeiro, seu sistema de coordenadas pode mudar de forma de uma maneira que o faça quebrar em certos pontos, assim como a latitude e a longitude falham nos polos. Tais pontos são chamados de “singularidades coordenadas” (para distingui-las das singularidades físicas, como um buraco negro real). Eles são pontos indefinidos em seu sistema de coordenadas que impossibilitam seguir uma solução em evolução durante todo o tempo.
Segundo, um sistema de coordenadas mal ajustado pode disfarçar os fenômenos físicos subjacentes que ele pretende medir. Para provar que as soluções para as equações de Einstein se estabelecem em um estado estável após serem perturbadas, os matemáticos devem manter um controle cuidadoso das ondulações no espaço-tempo que são acionadas pela perturbação. Para entender o porquê, vale a pena considerar a lagoa novamente. Uma rocha lançada em uma lagoa gera ondas. A estabilidade a longo prazo da lagoa resulta do fato de que essas ondas decaem com o tempo – elas crescem cada vez menores até que não haja sinais de que elas estejam lá.
A situação é semelhante para o espaço-tempo. Uma perturbação desencadeará uma cascata de ondas gravitacionais, e provar a estabilidade requer provar que essas ondas gravitacionais decaem. E provar a deterioração requer um sistema de coordenadas – chamado de “medidor” – que permite medir o tamanho das ondas. O medidor correto permite que os matemáticos vejam as ondas se achatarem e eventualmente desaparecerem completamente.
“A decadência tem que ser medida em relação a algo, e é aqui que a questão do medidor aparece”, disse Klainerman. “Se eu não estiver no medidor certo, mesmo que, em princípio, eu tenha estabilidade, não posso provar isso porque o medidor simplesmente não permite que eu veja essa decadência. Se eu não tiver taxas de ondas de decaimento, não posso provar a estabilidade. “
O problema é que, embora o sistema de coordenadas seja crucial, não é óbvio qual deles escolher. “Você tem muita liberdade sobre o que esta condição de medidor pode ser”, disse Hintz. “A maioria dessas escolhas vai ser ruim.”
Quase lá
Uma prova completa da conjectura da estabilidade do buraco negro requer provar que todas as soluções de buracos negros conhecidas para as equações de Einstein (com o spin do buraco negro abaixo de um certo limite) são estáveis após serem perturbadas. Essas soluções conhecidas incluem a solução Schwarzschild, que descreve o espaço-tempo com um buraco negro não rotativo, e a família de soluções Kerr, que descrevem configurações de espaço-tempo vazias de tudo, exceto um único buraco negro rotativo (onde as propriedades rotativas do buraco negro – sua massa e momento angular – variam dentro da família de soluções).
Ambos os novos resultados fazem progressos parciais em direção a uma prova da conjectura completa.
Hintz e Vasy, em um artigo postado no arXiv, site de pré-impressão científica em 2016, provaram que os buracos negros de rotação lenta são estáveis. Mas o trabalho deles não cobria buracos negros que giravam acima de um certo limite.
Sua prova também faz algumas suposições sobre a natureza do espaço-tempo. A conjectura original está no espaço de Minkowski, que não é apenas plano e vazio, mas também fixo em tamanho. A prova de Hintz e Vasy ocorre no chamado espaço de Sitter, onde o espaço-tempo está se acelerando, assim como no universo real. Essa mudança de configuração torna o problema mais simples do ponto de vista técnico, o que é fácil de apreciar em um nível conceitual: se você soltar uma pedra em uma lagoa em expansão, a expansão vai esticar as ondas e tornar a decadência mais rápida do que seria se a lagoa não estivesse se expandindo.
“Você está olhando para um universo em expansão acelerada”, disse Hintz. “Isso torna o problema um pouco mais fácil, pois parece diluir as ondas gravitacionais”.
O trabalho de Klainerman e Szeftel tem um teor ligeiramente diferente. A prova deles, a primeira parte da qual foi publicada online em novembro passado, acontece no espaço-tempo de Schwarzschild – mais perto do cenário original, e mais difícil para o problema. Eles provam a estabilidade de um buraco negro não rotativo, mas não abordam soluções nas quais o buraco negro está girando. Além disso, eles apenas provam a estabilidade das soluções de buracos negros para uma classe restrita de perturbações – onde as ondas gravitacionais geradas por essas perturbações são simétricas de uma certa maneira.
Ambos os resultados envolvem novas técnicas para encontrar o sistema de coordenadas correto para o problema. Hintz e Vasy começam com uma solução aproximada para as equações, com base em um sistema de coordenadas aproximado, e gradualmente aumentam a precisão de sua resposta até chegarem a soluções exatas e coordenadas bem comportadas. Klainerman e Szeftel adotam uma abordagem mais geométrica do desafio.
As duas equipes estão tentando construir seus respectivos métodos para encontrar uma prova da conjectura completa. Alguns observadores especialistas acham que o dia pode não estar longe.
“Eu realmente acho que as coisas estão agora no estágio em que as dificuldades restantes são apenas técnicas”, disse Dafermos. “De alguma forma, não é preciso ter novas ideias para resolver esse problema”. Ele enfatizou que uma prova final poderia vir de qualquer um dos muitos matemáticos que trabalham atualmente no problema.
Por 100 anos, as equações de Einstein serviram como um guia experimental confiável para o universo. Agora os matemáticos podem estar chegando mais perto de demonstrar exatamente por que eles funcionam tão bem.
