Equações diferenciais são usadas quando a taxa de variação (ou simplesmente a mudança) de uma função é conhecida, mas não a função em si. Essas equações são a base de grande parte da ciência e engenharia moderna e não é por acaso; no universo ‘mudança é a única constante’ como diria Heráclito. Seria de se esperar que equações diferencias fossem a língua franca de toda a ciência (e matrizes também, já que sem elas não é possível usar o MATLAB e sem o qual a vida não tem sentido). A realidade até que não está tão distante disso, mas como eu mesmo não canso de lembrar, existe uma notável exceção: as ciências sociais. Isso se deve em parte, é claro, à complexidade desse campo e da dificuldade em até mesmo definir quais são as variáveis relevantes. Até aí tudo bem; existem de fato muitos cientistas sociais competentes em matemática que aceitaram o desafio. Mas em contrapartida para cada um desses há talvez 10 outros que resistem por razões ideológicas. Várias correntes de pensamento nas ciências humanas são abertamente anti-científicas e hostis a qualquer tentativa de mensuração e formalização matemática. O resultado desse mix de complexidade por um lado e repulsa ideológica por outro é uma classe inteira de cientistas sem formação matemática. O exemplo que descrevo abaixo deixa claro as consequencias tragi-cômicas dessa infeliz situação.
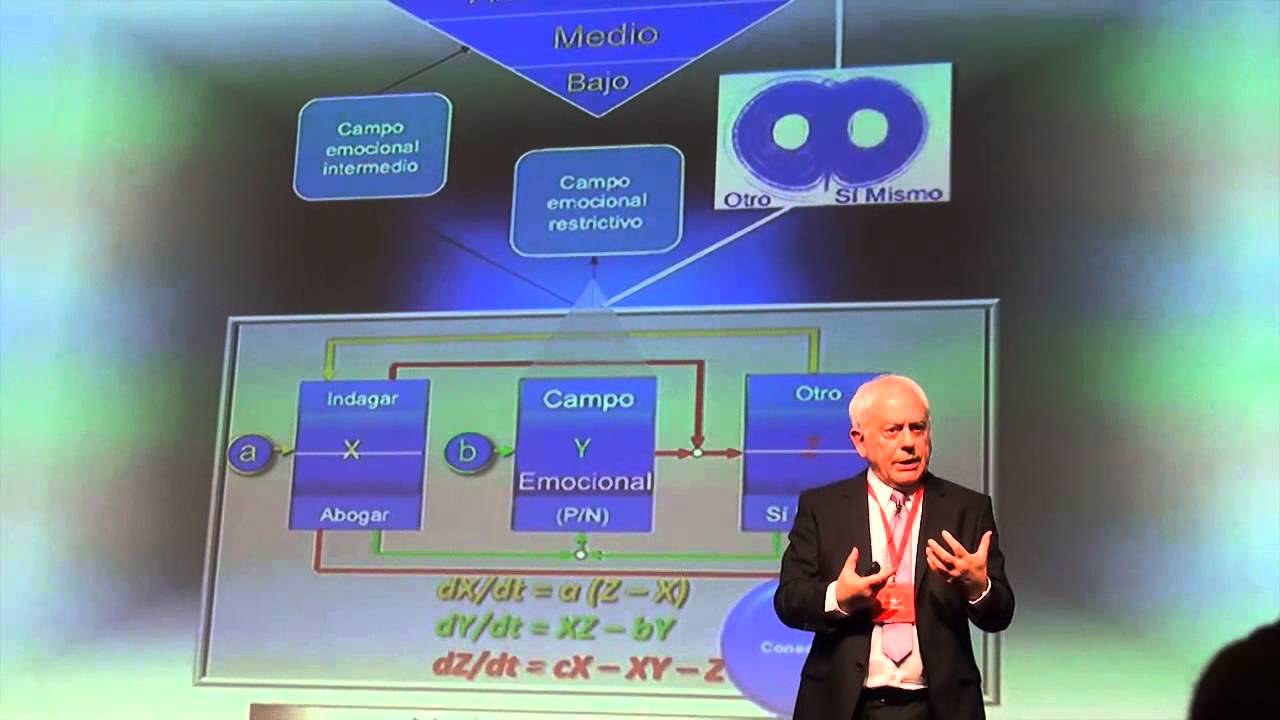
Imagine poder descrever o desenrolar das emoções humanas da mesma maneira que um físico descreve a dinâmica dos fluídos. Algumas equações diferenciais não-lineares, um rotineiro Runge Kutta de ordem 4 no MATLAB e pronto: toda a sutileza e variabilidade das emoções expressa em dois ou três plots bidimensionais. Agora imagine ainda descobrir que por uma grande coincidência cósmica essas equações são exatamente iguais as equações de Lorenz, as mesmas que descrevem o fenômeno da convecção em fluídos. Que exemplo mais lindo seria esse de generalização matemática unificando partes aparentemente tão distintas do cosmos: a física de fluídos e a psicologia humana.
Foi exatamente isso que Marcial Francisco Losada descobriu e publicou em 1999 no periódico Mathematical and Computer Modelling. Nesse paper Losada afirma ter feito essa descoberta ao observar em laboratório o comportamento de grupos de empresários realizando tarefas típicas do ambiente de negócios. Com base nesses dados Losada desenvolveu um modelo matemático não-linear que descreve as interações grupais e que coincidentemente também acontece de ser idêntico ao de Lorenz. Em 2004 Losada e Heaphy publicaram um outro paper onde usam o mesmo modelo para investigar o papel da conectividade e da razão entre emoções positivas e negativas (P/N) nas mesmas interações grupais. Finalmente em 2005, quando Losada trabalhava na Universidade Católica de Brasília, ele e Barbara L. Fredrickson alegaram ter derivado do mesmo modelo o que pode-se chamar de uma receita para a prosperidade e crescimento emocional, uma razão ótima entre positividade e negatividade: P/N=2.9. Com três emoções positivas para cada negativa você também pode atingir o sucesso emocional! E tudo provado com a mais sólida matemática de sistemas dinâmicos.
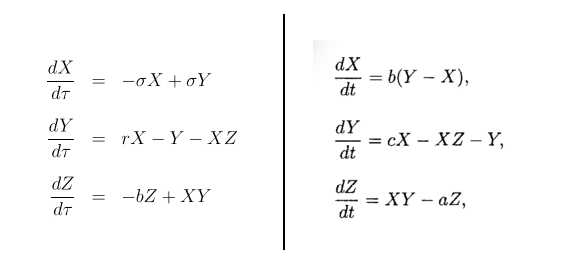
Se tudo isso soa demasiado fantástico para ser verdade, é porque deveria. No entanto todas estas alegações foram publicadas em bons periódicos e aceitas sem muitos problemas. Barbara Fredrickson, a co-autora do paper com o número mágico 2.9 do florescimento emocional é uma renomada professora de psicologia da University of North Carolina nos USA e autora de vários livros. O próprio paper de 2005 foi publicado na revista The American Psychologist e já recebeu mais de 1000 citações. Figuras eminentes da psicologia como Martin Seligman (que já foi presidente da American Psychological Association) não tardaram a divulgar entusiasticamente esses resultados.
Eis que entra em cena Nick Brown, um senhor de 50 anos aposentado da área de TI e cursando uma pós-graduação em psicologia em uma universidade pequena de Londres. Conta a lenda (ou melhor o The Guardian) que ao ver durante uma aula um slide com a teoria de Losada e Fredrickson, seu alarme cético disparou. Porém Brown não dominava matemática o suficiente para analisar sozinho o problema. O que ele faz a seguir é simplesmente épico: Brown entra em contato com nada mais nada menos que Alan Sokal, o famoso desbancador de besteiras pós-modernas. Sokal percebeu na hora que se tratava de mais uma impostura intelectual e, junto com Nick Brown e Harris Friedman, escreveu um artigo desmontando a história toda: os dados dos experimentos que supostamente levaram a criação do modelo nunca foram publicados, não há nenhuma justificativa teórica que possa sustentar tal modelo, a tentativa de aplicar as equações de Lorenz às emoções está cheia de erros matemáticos grosseiros e por aí vai.
É incrível que Losada tenha conseguido publicar em três grandes periódicos diferentes e que ninguém tenha notado nada de estranho nesse tempo todo. Sokal já tinha soado o alarme anos antes com a sua paródia na Social Text e com o seu magnífico desmonte das asneiras pós-modernas no subsequente ‘Imposturas Intelectuais’. Mas se o analfabetismo matemático continua atrapalhando o avanço da psicologia americana, no Brasil a dimensão do problema é muito maior. Com a maioria dos cursos de graduação ainda confundindo psicologia com psicanálise, o leitor pode tirar suas próprias conclusões.
Referências
- Brown, N. J. L., Sokal, A. D., & Friedman, H. L. (2013). The complex dynamics of wishful thinking: the critical positivity ratio. The American Psychologist, 68(9), 801–13. doi:10.1037/a0032850
- Fredrickson, B. L., & Losada, M. F. (2005). Positive affect and the complex dynamics of human flourishing. The American Psychologist, 60(7), 678–686.
- Losada, M. (1999). The complex dynamics of high performance teams. Mathematical and Computer Modelling, 30(9-10), 179–192. doi:10.1016/S0895-7177(99)00189-2
- Losada, M., & Heaphy, E. (2004). The Role of Positivity and Connectivity in the Performance of Business Teams: A Nonlinear Dynamics Model. American Behavioral Scientist, 47(6), 740–765. doi:10.1177/0002764203260208