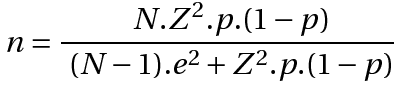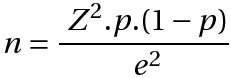No último dia 25, a Folha de São Paulo publicou uma reportagem mostrando dados de uma pesquisa de opinião realizada por seu instituto. Os destaque da matéria indica que cerca de nove entre dez brasileiros atribuem seu sucesso financeiro a Deus. Mas o que chamou muita atenção é que mesmo entre os ateus havia uma significativa taxa de concordância com essa afirmação, chegando a 23%.
Isso mesmo: a cada quatro ateus, um estaria atribuindo seu sucesso financeiro a Deus.
Em pouco tempo, os resultados começaram a ser comentados e ridicularizados em outros sites e nas redes sociais. Simultaneamente, pessoas tentavam entender o que aconteceu. Estariam os ateus mentindo ou brincando com os pesquisadores? Os dados foram forjados? As perguntas foram mal formuladas? O que explica números tão estranhos?
Pois bem. Alguns dias após a reportagem, o Datafolha publicou em seu site oficial a íntegra da pesquisa realizada, o que nos permitirá entender qual foi a causa de toda essa confusão.
Como funciona uma pesquisa de opinião?
Antes de qualquer coisa, precisamos entender como são feitos estudos desse tipo. A coisa toda está sustentada em uma premissa básica: quando temos uma grande população, nós podemos descobrir coisas sobre ela sem necessariamente estudar todos os seus elementos. Uma analogia irá facilitar o entendimento: imagine que seu médico precisa saber como está a contagem de leucócitos (glóbulos brancos) em seu sangue para fazer uma avaliação de seu sistema imunológico. Então você faz um exame onde alguns poucos mililitros são retirados e analisados em um laboratório. Dias depois, o médico te avisa: “não se preocupe, o número de leucócitos em seu sangue está em um nível excelente!” Para sua sorte, o laboratório não precisou recolher todo o seu sangue em uma máquina e contar os leucócitos um por um. Apenas uma fração mínima precisou ser analisada para que soubéssemos algo em relação ao todo.
Com uma população de seres humanos, não é diferente. Quando queremos saber, por exemplo, em quem as pessoas estão planejando votar na próxima eleição, não precisamos entrevistar todos os eleitores. Basta uma pequena amostra e ela nos dará informações relativas ao eleitorado completo.
Claro que não estamos falando de qualquer amostra. Para que os resultados sirvam para nosso propósito, ela precisa ser representativa. Quando dizemos que uma amostra é representativa, isso significa que ela tem uma chance altíssima, muito próxima de 100%, de preservar as características da população original. No caso das eleições, uma amostra representativa é aquela que tem grande probabilidade de preservar a preferência eleitoral da população. Para isso, geralmente se garante que a amostra preserve as mesmas proporções de pessoas de cada gênero, idade, etnia, região de origem, nível de renda, nível de escolaridade etc. da população total. Se estamos falando da população de eleitores do Brasil inteiro para analisar uma corrida presidencial, nossa amostra deve, de certa forma, ser uma réplica do eleitorado brasileiro. Com muito menos gente, mas de forma a imitar bem sua composição geral.
Outra regra muito importante para garantir que uma amostra seja representativa é o seu tamanho. Se por um lado não queremos entrevistar todos os membros da população, por outro também não podemos entrevistar um número muito reduzido.
Cálculo amostral
A quantidade mínima de pessoas que devem ser entrevistadas para que uma amostra seja representativa depende de vários fatores:
- O tamanho da população ou “universo” (“N”): obviamente, quanto maior a população que queremos representar, maior será o número de pessoas da amostra. Contudo, essa relação não é linear. Ainda que o tamanho da amostra aumente quando a população aumenta, sua proporção em relação ao total diminui.
- A margem de erro (“e”): nós nunca podemos calcular qual a proporção exata da população que está em cada segmento. O que é feito é criar uma faixa de valores em torno da proporção calculada, dada em pontos percentuais, onde a proporção real deve estar contida. A margem de erro mais adotada pelos institutos de pesquisa é de dois pontos percentuais para mais ou para menos. Isso significa que se eu disser “o candidato A possui 35% das intenções de voto do eleitorado”, na verdade estou querendo dizer o seguinte: “o candidato A possui entre 33% e 37% das intenções de voto do eleitorado”. É por isso que quando a diferença entre dois candidatos é menor que dois pontos percentuais, diz-se que houve empate técnico: como as faixas de valores de ambos acabam se sobrepondo, a pesquisa se torna incapaz de dizer quem está na frente.
- O nível de confiança: geralmente adotado como sendo de 95%, pode ser entendido de duas formas equivalentes. Uma delas é dizendo que se o levantamento fosse repetido 100 vezes, em 95 delas os resultados estariam contidos dentro da margem de erro. Outra forma de dizer a mesma coisa é que, na população real, há uma probabilidade de 95% de os resultados estarem coerentes com os encontrados, dentro da margem de erro. Usando o nível de confiança é calculado um valor crítico geralmente escrito como Z. Como é complicado calcular Z toda vez, seu valor costuma ser tabelado e vir como apêndice em livros de estatística. Também pode ser encontrado facilmente na internet.
- Para refinar nossa amostra, podemos ainda acrescentar no modelo informações já conhecidas sobre a população. Por exemplo, se queremos calcular a porcentagem de pessoas de ascendência oriental na população brasileira, podemos assumir algo como: “eu tenho certeza de que essa porcentagem é menor que 50%”. Equipar o modelo com essa premissa, que parece bastante correta, ajudaria a diminuir um pouco o número de pessoas entrevistadas. Entretanto, não trabalharemos aqui com esse tipo de suposição. A variável associada a esse valor suposto é notada como “p”, que é padronizada como 0,5 em um modelo totalmente livre de suposições.
Esclarecidas as variáveis, podemos calcular o tamanho mínimo n de uma amostra representativa através da seguinte fórmula:
Quando a população que estamos estudando é muito grande, tipicamente acima de 100 mil elementos (estatísticos são um pouco exagerados e chamam essas populações de “infinitas”), o segundo termo do denominador torna-se insignificante em relação ao primeiro, e o quociente N/(N-1) torna-se muito próximo de 1. Ambos podem, portanto, ser omitidos:
O que foi que aprontaram então?
Através da pesquisa completa, podemos perceber que a população que o estudo tem como alvo está muito bem definida: é a população brasileira com 16 anos ou mais. Em outras palavras, a amostra escolhida tem o objetivo de representar esse contingente de cerca de 140 milhões de pessoas (sabermos o número exato é desnecessário pois uma pequena diferença em números dessa magnitude – e mesmo uma diferença razoável de alguns milhões – é insignificante para o escopo deste cálculo, como você pode conferir).
Também é dito que a margem de erro adotada foi de 2 pontos percentuais e que o nível de confiança é de 95%, típico da maioria das pesquisas de opinião.
Nada é falado sobre a adoção de premissas que possam alterar o valor da variável p. Portanto, podemos supor que o adotado é o padrão de 0,5.
Para saber o valor mínimo que a amostra precisa ter, você pode calcular manualmente através da fórmula. Ou, caso seja adepto das maravilhosas facilidades da tecnologia moderna, utilizar uma das calculadoras de amostra que podem ser encontradas na internet:
OPÇÃO 2 (não preencher os percentuais máximo e mínimo, para garantir p = 0,5)
OPÇÃO 3 (escolher a opção “mais heterogênea”, pelo mesmo motivo acima)
De qualquer forma, chegamos à conclusão de que a amostra deve ter tamanho mínimo de 2401 pessoas. Como o número de entrevistas relatado no estudo é de 2828, podemos afirmar que a amostra possui tamanho adequado.
É agora que vem o grande detalhe: adequado para quê?
A amostra do estudo possui tamanho suficiente para suportar as afirmações que são feitas sobre o universo de 140 milhões de brasileiros maiores de 16 anos, mas isso não significa que ela autoriza conclusões em relação a sub-grupos dessa população. Ainda que o “Brasil adulto” esteja representado na pesquisa e que informações consistentes possam ser colhidas sobre esse contingente de pessoas, nada pode ser dito sobre “os ateus”, “os umbandistas”, “os moradores do Sul”, “os inclusos em certa faixa de renda” ou qualquer conjunto menor contido no todo. Pegar uma amostra verdadeiramente significativa da população e depois dividi-la em grupos menores não garante que esses grupos menores também sejam, por sua vez, significativos em relação à característica que representam. As únicas coisas que podem ser ditas com segurança no estudo do Datafolha são aquelas sobre “os brasileiros maiores de 16 anos”. Essa é a população do estudo. Tudo que for referente a outros grupos contidos não está devidamente justificado pelos dados.
Se nós quisermos saber algo especificamente sobre as opiniões dos ateus brasileiros maiores de 16 anos, o raciocínio usado precisa ser o seguinte:
Quantos deles há no Brasil? Vamos usar um número bem conservador. Segundo o censo de 2010 do IBGE, os ateus eram na época 615 mil pessoas no Brasil (outros levantamentos apontam números bem maiores). Esse valor deve ter aumentado, mas vamos deixar assim. Desses, vamos ainda considerar que menos da metade esteja acima de 16 anos. Ou seja, que esse grupo forme uma população de apenas 300 mil pessoas. Estamos realmente sendo muito generosos nessa estimativa.
Agora vamos calcular qual o tamanho mínimo de uma amostra representativa desses 300 mil elementos, mantendo iguais os demais parâmetros. Coloque os dados na fórmula ou em alguma das calculadoras e você verá que, para dizer qualquer coisa sobre a opinião deles, deveriam ter sido entrevistados 2382 ateus maiores de 16 anos.
E quantos o Datafolha entrevistou? Apenas 38!
Você pode conferir isso na página 17 do estudo completo. Existe uma tentativa de estabelecer as opiniões de 300 mil pessoas através da consulta a apenas 38. Com uma amostra tão pequena, tão longe do valor mínimo para obter alguma significância, fica fácil entender por que apareceram conclusões inesperadas. Sem o cuidado de perceber que as amostras não são significativas, podemos achar coisas até mais engraçadas do que a questão envolvendo sucesso financeiro. Se olharmos nas páginas 172 e 173, veremos pérolas como:
Afirmação: “O homem é uma criação de Deus, que o construiu à sua imagem e semelhança.”
21% dos ateus concordam, 56% discordam.
Afirmação: “Aqueles que creem em Deus, quando morrerem, irão para o Céu e terão uma vida eterna.”
21% dos ateus concordam, 64% discordam.
Afirmação: “O fim do mundo está próximo e somente aqueles que acreditam em Deus irão se salvar.”
12% dos ateus concordam, 72% discordam.
Tudo isso, claro, tendo como base a mesma amostra irrisória de 38 elementos. Considere ainda que parte desses ateus podem ser, na verdade, falsos positivos resultantes de erros muito pontuais na aplicação do questionário e as anomalias estão explicadas.
O problema deveria ter sido evitado aí. Um jornalista cuidadoso jamais poderia veicular informações que não são suportadas pela pesquisa. Deveria suspeitar quando visse um número tão inesperado em meio aos demais. Da mesma forma, os estatísticos responsáveis deveriam prevenir explicitamente que esse tipo de interpretação pudesse ser extraída de seus dados.
O que aprendemos com isso?
A estatística é um campo de conhecimento de extrema utilidade. É difícil superestimar como a boa interpretação dos dados pode melhorar a sociedade em que vivemos, aumentando o conhecimento que temos de nossos próprios problemas e ainda nos guiando às melhores soluções para resolvê-los. Por outro lado, está cheia de armadilhas que têm enganado pessoas muito perspicazes ao longo dos anos. Às vezes o problema sequer está em um erro metodológico. Mesmo estatísticas baseadas em populações inteiras ou amostras realmente significativas, sem vieses propositais ou erros grosseiros, podem levar a falhas de entendimento e interpretação. Os dados estão aí, mas o que fazemos com eles é responsabilidade nossa.
Em seu best-seller “Como mentir com estatística”, no longínquo ano de 1954, Darrell Huff já nos premiava com um sábio conselho:
“‘Isso faz sentido?’ reduzirá frequentemente uma estatística ao seu valor real, quando toda a conversa fiada estiver se baseando numa suposição sem provas.”