Por Christian Rothleitner
Publicado na Nature
Quatro forças fundamentais são conhecidas na física: as interações fracas e fortes e as forças eletromagnéticas e gravitacionais. A força gravitacional é a mais fraca dessas quatro. Por esta razão, e pelo fato dos experimentos não poderem ser protegidos da gravidade da Terra, as medições do campo gravitacional de um objeto testado são difíceis de serem realizadas em laboratório – mesmo para objetos com massas de vários quilogramas. Mas em um estudo publicado na Nature, Westphal et al. relatou a detecção do acoplamento gravitacional entre duas massas de apenas cerca de 90 miligramas.
As interações fracas, fortes e eletromagnéticas foram unificadas no modelo padrão da física, mas a força gravitacional não pode ser integrada a esse modelo. O melhor modelo atualmente disponível para descrever a gravidade é a teoria da relatividade geral. Essa teoria não falhou em nenhum teste até agora, mas há algo estranho nela pois ela não pode ser explicada em termos de mecânica quântica.
Para a maioria dos propósitos científicos, entretanto, não precisamos usar a teoria da relatividade geral para explicar a gravidade – a lei da gravitação universal de Isaac Newton funciona perfeitamente. Publicada em 1687, a lei de Newton afirma que a atração gravitacional entre dois corpos é proporcional às suas massas e inversamente proporcional ao quadrado da distância entre eles. Isso provou ser correto não apenas para descrever a maioria das observações astronômicas, mas também em experimentos de laboratório. Por exemplo, a trajetória de um objeto em queda livre (como uma maçã caindo de uma árvore) pode ser medida com uma precisão de menos de dez partes em um bilhão, e os resultados estão de acordo com o que seria esperado da lei de Newton.
Durante o século XX, no entanto, surgiram questões sobre uma correção geral desta lei: uma distribuição anômala da velocidade das estrelas nas galáxias foi observada no início dos anos 1930, e não poderia ser explicada usando apenas a lei de Newton. Mesmo a teoria da relatividade geral não pode explicar esse fenômeno. Uma explicação é postular a existência de matéria escura – um componente invisível do Universo, mas gerador de gravidade. No entanto, ninguém sabe realmente do que é feita essa matéria escura.
Outra explicação, que é controversa, mas mais fácil de integrar em modelos do que a matéria escura, é que a lei gravitacional de Newton precisa de uma correção. Uma teoria que tenta tal correção foi proposta na década de 1980 e é chamada de dinâmica newtoniana modificada. A base desta teoria é que a força do campo gravitacional (a aceleração devido à gravidade) não segue a lei do inverso do quadrado de Newton em grandes distâncias.
Um outro mistério é que a força gravitacional é cerca de 36 ordens de magnitude mais fraca do que a força eletromagnética. Isso é chamado de problema de hierarquia.
Uma estrutura conhecida como teoria das cordas, que foi desenvolvida em parte para fornecer uma descrição teórica quântica da gravidade, aborda esse problema ao propor que há mais dimensões espaciais do que as três que podemos observar. A gravidade – ao contrário das três outras forças fundamentais – permeia essas dimensões extras. Se for verdade, então isso poderia explicar por que a força gravitacional é muito mais fraca do que a força eletromagnética. Outra consequência seria que, ao longo de uma certa faixa espacial, a força gravitacional não pode ser descrita pela lei do inverso do quadrado de Newton.
Outra coisa peculiar sobre a gravidade é que as medições independentes da constante gravitacional de Newton (G, uma constante fundamental usada em cálculos de efeitos gravitacionais) variaram amplamente. Determinações experimentais de outras constantes fundamentais, como a constante de Boltzmann ou a velocidade da luz, convergiram conforme o número e a precisão das medições aumentaram. Isso não aconteceu através de G.
Os experimentos de Westphal e seus colegas podem nos levar um passo mais perto de compreender os mistérios da gravidade. Eles investigaram a força gravitacional usando uma versão em miniatura de uma balança de torção – um dispositivo que foi usado pela primeira vez por Henry Cavendish em 1798 para medir a densidade da Terra (um experimento que é equivalente a medir G), e que ainda é o dispositivo padrão-ouro para determinar G.
Uma balança de torção consiste em uma barra horizontal suspensa no meio por um fio pendurado verticalmente e com massas de teste presas às extremidades. A atração gravitacional da Terra atua na direção vertical, ao longo da qual o fio apresenta uma grande rigidez. Mas na direção horizontal, o fio é facilmente torcido e tem uma constante de mola minúscula – forças muito fracas aplicadas em ângulos retos na barra causam grandes rotações da barra. A balança, portanto, gera um ambiente quase livre de gravidade (descrito com mais precisão como microgravidade) no plano horizontal. Isso é perfeito para detectar pequenas forças, como a atração gravitacional exercida na barra por um objeto próximo (a massa de origem).
Em determinações típicas de G, as massas de origem eram pesadas (vários quilogramas), para compensar a fraqueza da força gravitacional. Em contraste, Westphal e colegas de trabalho usaram esferas de ouro apenas 92 miligramas em massa (Fig. 1), aproximadamente a massa de 4 moscas domésticas. Esta é a menor massa de origem já usada em tal experimento.
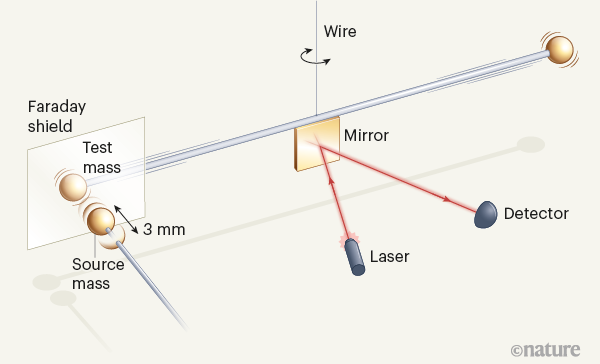
Um cálculo usando a lei da gravitação de Newton mostra que a força agindo entre duas massas esféricas de 90 mg com uma separação do centro de massa de 2,5 milímetros (aproximadamente os parâmetros do experimento de Westphal et. al) é apenas cerca de 9×10-14 newtons. Esta é aproximadamente a mesma força que atua sobre uma massa de 9 picogramas (1 pg é 10-12 g) no campo gravitacional da Terra; para colocar isso em perspectiva, 9 pg é cerca de um terço da massa de um glóbulo vermelho humano. O grande desafio era, portanto, extrair este sinal gravitacional extremamente pequeno do ‘ruído’ de fundo no experimento e dos efeitos de outras forças (como interações eletromagnéticas) que se tornam mais fortes do que as forças gravitacionais quando a fonte e as massas de teste são separadas por pequenas distâncias.
Westphal et al. portanto, modulou o sinal variando periodicamente a posição da massa de origem em relação à massa de teste na balança de torção. Como consequência da interação gravitacional dependente do tempo, o equilíbrio oscilou no plano horizontal na frequência de modulação do sinal (12,7 milihertz). Como o campo gravitacional de uma massa esférica não é linear (uma consequência da lei do inverso do quadrado de Newton), o equilíbrio também é estimulado a oscilar em frequências mais altas que são múltiplas da frequência de modulação (conhecidas como harmônicas mais altas). Esse efeito pôde ser claramente identificado no experimento, fornecendo assim um sinal do acoplamento gravitacional entre as massas.
A detecção de um sinal gravitacional tão minúsculo é em si um resultado empolgante, mas os autores foram ainda mais longe ao determinar um valor para G a partir de seu experimento. Suas estimativas desviam do valor acordado internacionalmente em cerca de 9% – uma pequena quantidade, dado que as incertezas experimentais do seu sistema não foram ainda otimizadas para medições precisas de L. O experimento é, portanto, o primeiro a mostrar que a lei da gravidade de Newton é válida até mesmo para massas de origem tão pequenas quanto essas.
O próximo passo é avançar para massas ainda menores – Westphal et al. sugerem que campos gravitacionais de massas da ordem de 10-8 kg podem eventualmente ser medidos. No entanto, muito trabalho precisará ser feito para atingir esse objetivo. A primeira tarefa será reduzir substancialmente o amortecimento das oscilações da balança de torção, o que não será fácil. Mas se isso puder ser feito, talvez os efeitos gravitacionais quânticos sejam finalmente observados.





