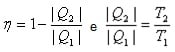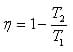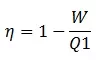Esse será um sistema termodinâmico que iremos ver muito a partir de agora, desenvolvido por Nicolas Carnot em meados do século XIX, ele propôs uma maquina térmica teórica que trabalhasse em um sistema ideal, que conseguisse alcançar o maior rendimento possível para os padrões adotados, que mais tarde foi chamada de Ciclo de Carnot.
Para eu poder explicar com clareza é importante que você já tenha em mente os conceitos que já abordamos no artigo anterior, além de um conhecimento prévio, porém básico de matemática.
Eu quero ressaltar que a importância desse ciclo para o estudo das engenharias e para a melhor compreensão das Leis da Termodinâmica, e por se tratar desse módulo, quero frisar também que o ciclo opera de acordo com a termodinâmica, e por isso iremos estudá-lo como sendo um ciclo ideal, portanto reversível.
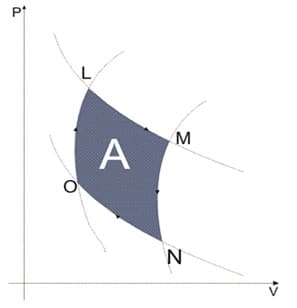
Este ciclo é composto de quatro processos que independente das substâncias, que iremos analisar através desse diagrama PV.
- Uma compressão isotérmica reversível, o processo sede calor ao sistema (N-O).
- Uma compressão adiabática reversível, o processo não troca calor com a vizinhança (O-L).
- Uma expansão isotérmica reversível, o processo recebe uma quantidade de calor dos processos (L-M).
- Uma expansão adiabática reversível, o sistema não troca calor com a vizinhança (M-N).
Existe outro diagrama que pode facilitar a compreensão do ciclo para aqueles que são familiarizados com gráficos.
Ciclo de Carnot Direito
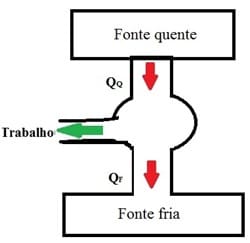
Existem duas fontes de calor, Fonte Quente (FQ) com uma temperatura T1, e a Fonte Fria (FF) com uma temperatura T2.
A FQ fornece calor (Q1) que é convertida em trabalho (W) por um mecanismo, como há uma diferença de temperatura parte do calor fornecido de FQ1 é descartado para a vizinhança, FF, tornando-se Q2, fechando assim o ciclo.
Espero que vocês tenha conseguido perceber os processos, as setas servem para poder compreender onde cada processo ocorre.
Agora vamos desenvolver a parte logico matemática.
Numa máquina de Carnot, a quantidade de calor que é fornecida pela fonte de aquecimento e a quantidade cedida à fonte de resfriamento são proporcionais às suas temperaturas absolutas, assim:
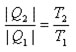
T₂ = temperatura absoluta da fonte de resfriamento
T₁ = temperatura absoluta da fonte de aquecimento
Observem que está sendo divididas temperaturas absolutas (ou seja, em escala Kelvin), portanto o resultado é adimensional, podendo ser convertido em porcentagem.
Agora vamos a exemplos práticos? E você vai achar bem interessante o estudo de caso que selecionei.
Imagine que você tem um carro com um motor 1.0, e que está 28°C onde você se encontra ao dar a partida no carro, bem se sabe que motores trabalham a um faixa de temperatura acima de 85°C e podendo a chegar até 90°, tenha esses valores em mente, irei selecionar as para T₁ = 87°C e para T₂ = 28°C onde T₂ é o meio externo. Vamos começar a calcular? Você pode fazer o seu próprio calculo de acordo com as temperaturas que você preferir.
O primeiro passo é converter as temperaturas em Celsius para Temperaturas absolutas Kelvin, para fazer isso basta somar 273,15.
T₁ = 87°C + 273,15 = 360,15K
T₂ = 28°C + 273,15 = 301,15 K87
Com os valores convertidos vamos aos cálculos fornecidos por Carnot.
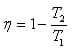
16%
E o que esse valor representa? Bem, você abastece com um determinado combustível, que ao ser queimado ele gera certa quantidade de energia térmica (Q), e de toda essa energia 16% dela foi convertida em trabalho, isso para um motor ideal, e para onde foi o resto da energia? Convertida em demais energia ao decorrer do processo, e isso acontece graças à entropia, ela é a responsável pela “perda” de energia no decorrer do ciclo, onde ela se apresenta? Bem no atrito entre os componentes do motor, no arrefecimento do motor, na diferença de potencial químico, nas conduções, radiação e convecção do calor e por ai vai, o que eu quero que vocês entendam que é jamais uma máquina irá converter toda uma energia na qual ela opere em trabalho, e que nunca uma máquina real, irá chegar aos valores da maquina teórica de Carnot, porque Carnot é um ciclo termodinâmico ideal. Caso aconteça dos intervalos de temperatura dar um resultado acima de 100% ela é inoperante e irreal para o mundo real e teórico.
OBS: Os valores adotados são apenas ilustrativas, motores comerciais tem o desempenho aproximado a 42% para um Ciclo de Carnot, esse valor diminui para o mundo real, chegando a uma faixa de 35%.
OBS2: Os reais valores de T em um motor de combustão interna estão muito além dos adotados acima, adotei os valores a seguir somente para fins didáticos e para facilitar a compreensão.
Agora vamos o Ciclo de Carnot Inverso, responsável pelos ciclos de refrigeração, que é basicamente igual, porém com parâmetros de processos inversos.
Ciclo de Carnot Inverso
Bem no Ciclo de Carnot Direito vimos que temos uma fonte de calor, responsável por ceder energia para um mecanismo para ele então assim realizar trabalho, no Ciclo de Carnot Inverso ou Ciclo de Carnot de Refrigeração é o contrario, eu tenho um foco frio, e quero retirar calor dele para jogar ao um foco quente, e para isso eu tenho que fornecer potência. Se você estiver pensando em um exemplo para compreender isso, bem existe um aparelho bem comum nas casas dos brasileiros que desenvolve esse papel muito bem, a geladeira, o ar-condicionado é outro, vamos à compreensão do ciclo.
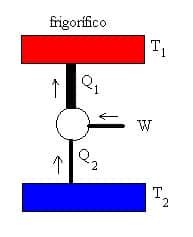
Repare que as setas mudaram de sentido.
Logo a formula do rendimento pra o Ciclo de Carnot inverso é:

Vou usar o exemplo de um aparelho de ar-condicionado. Muitas pessoas chegam ao vendedor e perguntado pela quantidade de BTUS de um aparelho visando economia e potencia, mas esse ideia está equivocada em ambos os pensamentos, o que você deve se preocupar ao comprar um ar-condicionado é o CoP – Coeficiente de Performance – somente algumas empresas disponibilizam a informação ao fornecedor em suas etiquetas, mas o calculo é muito simples de se realizar, porém precisa de umas conversões.
Um ar de 12.000 BTUs opera com a potencia de 1.6KW, temos que converter BTUS para KW e assim realizar a conta.
12.000 BTUS são equivalente a 3.52KW, basta realizar a divisão agora, o resultado será de:
2.2
Reparem que o numero deu maior do que um, e está correto, lembre-se é um ciclo inverso! Mas o que esse valor representa? Simples para cada unidade de energia elétrica que o aparelho consome, ele retira 2.2 unidades de calor, ou seja, quanto maior esse valor melhor, mas lembre-se, isso é um Ciclo de Carnot! O valor ai está para um maquina teórica ideal.
Ou seja, na próxima vez que você for comprar um aparelho de ar-condicionado procure saber o seu CoP.
Por enquanto vamos ficar por aqui com o Ciclo de Carnot, mas em breve vou dá mais explicações de como melhorar esses desempenhos.