Por Sean Carroll
Publicado no Preposterous Universe
Outro dia eu me diverti ao encontrar uma citação de Einstein, de 1936, sobre o quão difícil seria quantificar a gravidade: “[É] como uma tentativa de respirar no espaço vazio”. Oito décadas mais tarde, eu acho que ainda podemos concordar que é difícil.
Então aqui está uma possibilidade que vale a pena considerar: em vez da quantização da gravidade, talvez devêssemos tentar “gravitizar” a mecânica quântica. Ou, mais precisamente, mas menos sugestivamente, “encontrar a gravidade dentro da mecânica quântica”. Ao invés de começar com alguma visão essencialmente clássica da gravidade e “quantificá-la”, poderíamos nos imaginar começando com uma visão quântica da realidade desde o início, e encontrar o espaço tridimensional ordinário em que vivemos, de alguma forma, emergindo da informação quântica. Esse é o projeto que ChunJun (Charles) Cao, Spyridon (Spiros) Michalakis, e eu fizemos, com alguns passos hesitantes em direção em um novo paper.
Nós, seres humanos, mesmo aqueles que têm estudado a mecânica quântica por um longo tempo, ainda pensamos em termos de conceitos clássicos. Posições, momentos, partículas, campos, o próprio espaço. A mecânica quântica conta uma história diferente. O estado quântico do universo não é uma coleção de coisas distribuídas através do espaço, mas algo chamado de função de onda. A função de onda nos dá uma forma de calcular os resultados das medições: sempre que medimos uma quantidade observável como a posição, o momento ou a rotação de uma partícula, a função de onda tem um valor para cada resultado possível, e a probabilidade de obter esse resultado é dada pela função de onda ao quadrado. Na verdade, essa é normalmente a forma de construir funções de onda, na prática. Comece com alguma noção clássica real como “a posição de uma partícula” ou “a amplitude de um campo” e, para cada valor possível, anexe um número complexo. Esse número complexo, ao quadrado, nos dá a probabilidade de observar o sistema com que o valor é observado.
Matematicamente, funções de onda são elementos de uma estrutura matemática chamada de espaço de Hilbert. Isso significa que eles são vetores – podemos acrescentar estados quânticos em conjunto (a origem de sobreposições na mecânica quântica) e calcular o ângulo (“produto escalar”) entre eles. (Nós estamos saltando alguns detalhes técnicos aqui, especialmente em relação a números complexos – veja, por exemplo, o livro The Theoretical Minimum para mais). A palavra “espaço” no “espaço de Hilbert” não significa que o bom e velho espaço tridimensional que estamos acostumados, ou mesmo que seja o espaço-tempo quadridimensional da relatividade. É apenas uma maneira matemática de falar sobre “uma coleção de coisas”, neste caso, “possíveis estados quânticos do universo”.
O espaço de Hilbert é uma coisa bastante abstrata, o que pode parecer, às vezes, muito afastado dos fenômenos tangíveis de nossas vidas diárias. Isto leva algumas pessoas a se perguntar se precisamos complementar a mecânica quântica comum por novas variáveis adicionais, ou, alternativamente, imaginar que as funções de onda refletem nosso conhecimento sobre o mundo, ao invés de ser representações da realidade. Para os fins deste post, eu vou tomar o ponto de vista simples que a mecânica quântica diz que o mundo real é melhor descrito por uma função de onda, um elemento do espaço de Hilbert, evoluindo ao longo do tempo. (E o tempo do curso pode ser emergente, também… algo que deixarei para outro dia).
Aqui está a coisa: podemos construir um espaço de Hilbert, iniciando com uma ideia clássica como “todas as posições possíveis de uma partícula” e anexando um número complexo a cada valor, obtendo uma função de onda. Todas as funções de formas de onda concebíveis constituem o espaço de Hilbert que nos interessa. Mas não temos de fazê-lo dessa forma. Como Einstein poderia ter dito, “Deus não faria dessa forma”. Uma vez que tornamos funções de onda quantizandas em algum sistema clássico, temos estados que vivem no espaço de Hilbert. Neste ponto, essencialmente, não importa de onde viemos; agora nós estamos no espaço de Hilbert e deixamos nosso ponto de partida clássico para trás. Na verdade, é bem conhecido que muitas teorias clássicas diferentes levam à mesma teoria quando quantizadas, como também algumas teorias quânticas não tem antecessores clássicos, em tudo.
O mundo real é simplesmente a mecânica quântica, desde o início; não é uma quantização de algum sistema clássico. O universo é descrito por um elemento do espaço de Hilbert. Todas as nossas noções clássicas habituais devem ser derivadas disto, não o contrário. Mesmo o próprio espaço. Pensamos no espaço através do qual nos movemos como um dos componentes mais básicos e irredutíveis do mundo real, mas pode ser melhor pensado como uma noção aproximada que emerge a grandes distâncias e a baixas energias.
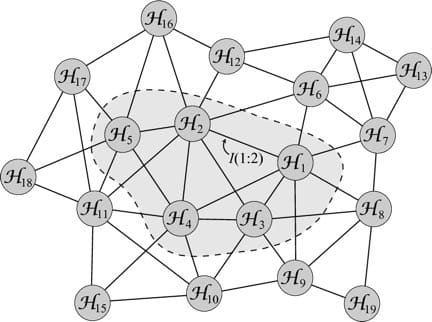
Então aqui está a tarefa que estabelecemos para nós mesmos: comece com um estado quântico no espaço de Hilbert. Não é um estado aleatório ou genérico, claro; É um tipo particular de estado. Divida o espaço de Hilbert em pedaços – tecnicamente, fatores que se multiplicam em conjunto para fazer todo o espaço. Use a informação quântica – em particular, a quantidade de emaranhamento entre diferentes partes do estado, medidos pela informação mútua – para definir uma “distância” entre elas. Peças que são altamente emaranhadas são consideradas próximas, enquanto as peças não-emaranhadas ficarão longe. Isto nos dá um grafo, onde os vértices são as diferentes partes do espaço de Hilbert, e as bordas são ponderadas pela distância emergente entre eles.
Podemos, então, fazer duas perguntas:
- Quando diminui-se o zoom, se o grafo assumir a geometria de um espaço liso, será liso com um número fixo de dimensões? (Resposta: sim, quando colocamos inicialmente um tipo certo de estados).
- Se perturbarmos o estado um pouco, qual será a mudança de geometria emergente? (Resposta: Curvas espaciais em resposta a massa/energia emergentes, de forma que lembrará a equação de Einstein na relatividade geral).
É essa última parte que é a mais emocionante, mas também a mais especulativa. A alegação, na sua forma mais dramática de sonoridade, é que a gravidade (curvatura do espaço-tempo causada pela energia/dinâmica) não é difícil de se obter na mecânica quântica – é automática! Ou, pelo menos, é a coisa mais natural de se esperar. Se a geometria é definida por emaranhamento e informação quântica, em seguida, perturbar o estado (por exemplo, pela adição de energia) muda naturalmente a geometria. E, se o modelo de jogos for em uma teoria de campo emergente a grandes distâncias, a relação mais natural entre a energia e a curvatura será dada pela equação de Einstein. A visão otimista é que a gravidade só aparece sem esforço no limite clássico de um sistema quântico apropriado. Mas “o demônio está nos detalhes”, e há um longo caminho a percorrer antes que possamos declarar vitória.
Aqui está o resumo para o nosso paper:
Space from Hilbert Space: Recovering Geometry from Bulk Entanglement
ChunJun Cao, Sean M. Carroll, Spyridon Michalakis
Examinamos como construir um coletor espacial e sua geometria da estrutura de emaranhamento de um estado quântico abstrato no espaço de Hilbert. Dada uma decomposição do espaço de Hilbert H em um produto de tensor de fatores, consideramos uma classe de “estados com restrições de redundância” em H que generaliza o comportamento área-lei para a entropia do emaranhamento, normalmente encontrado em sistemas de matéria condensada com Hamiltonianas locais com quebras. Usando a informação mútua para definir uma medida de distância no grafo, empregamos escalonamentos multidimensionais clássicos para extrair a dimensionalidade espacial com um melhor ajuste da geometria emergente. Em seguida, mostramos que as perturbações de emaranhamento em tais geometrias emergentes naturalmente dão origem a modificações locais de curvatura espacial que obedecem a um análogo (espacial) da equação de Einstein. O espaço de Hilbert correspondente a uma região de espaço plano e possui dimensão finita, e é ajustada à medida do volume, embora as escalas de entropia (e a alteração máxima da mesma) sejam como a área da fronteira. Uma versão da ER = conjectura da EPR recuperada, em que as perturbações que enredam partes distantes da geometria emergente geram uma configuração que possa ser considerada como uma fenda espacial altamente quântica.
Como quase todo o papel da física, estamos construindo algo sobre ideias que vieram antes. A ideia de que a geometria do espaço-tempo está relacionada com o emaranhamento tem se tornado cada vez mais popular, embora, na maior parte, tenha sido explorada no contexto holográfico da correspondência AdS/CFT; aqui estamos trabalhando diretamente na região “agrupada” de espaço, não é algo atraente para um limite distante. Uma noção relacionada é a conjectura ER= EPR de Maldacena e Susskind, relacionando o entrelaçamento com buracos de minhoca. Em certo sentido, estamos fazendo esta proposta um pouco mais específica, dando uma fórmula para a distância em função do emaranhamento. A relação de geometria para a energia vem de algo chamado de Primeira Lei do Emaranhamento, articulada por Faulkner et al., E é utilizada por Ted Jacobson em uma versão da Gravidade Entrópica. Mas, tanto quanto nós sabemos, nós somos os primeiros a iniciar diretamente no espaço de Hilbert, ao invés de assumir variáveis clássicas, uma fronteira, ou um espaço-tempo de fundo. (Há uma enorme quantidade de trabalho que tem sido feito em áreas estreitamente relacionadas, obviamente, então eu adoraria ouvir sobre qualquer coisa em particular que devam conhecer).
Somos rápidos em admitir que o que temos feito aqui é extremamente preliminar e conjectural. Não temos uma completa teoria de tudo, e até mesmo o que temos envolve uma grande quantidade de especulação e não de cálculos ainda suficientemente rigorosos.
Mais importante ainda, temos assumido que partes do espaço de Hilbert que são altamente emaranhadas também são “próximas”, mas não temos realmente derivado esse fato. É certamente o que deve acontecer, de acordo com nossa compreensão atual da teoria quântica de campos. Pode parecer que partículas entrelaçadas possam ser tão distantes quanto quiser, mas a contribuição das partículas para o entrelaçamento global é quase completamente insignificante – é o próprio vácuo quântico que carrega quase todo o emaranhamento, e é assim que obtemos a nossa geometria.
Mas continuará a ser visto se esta noção realmente corresponder ao que nós pensamos como “distância”. Para fazer isso, não é suficiente falar sobre o espaço, nós também precisamos falar sobre o tempo, e como estados evoluem. Esse é um próximo passo óbvio, mas nós apenas começamos a pensar sobre. Isto levanta uma variedade de perguntas intimidantes: Qual é o hamiltoniano apropriado que realmente gera a evolução temporal? O tempo é fundamental e contínuo, ou emergente e discreto? Podemos derivar uma teoria emergente que inclua não só o espaço curvo e o tempo, mas outros campos quânticos? Será que esses campos satisfazem a condição relativista de ser invariante sob as transformações de Lorentz? Será que a gravidade, em particular, têm propagação correspondente com graus de liberdade para girar 2 grávitons? (E apenas um tipo de gráviton, unido universalmente à energia-momentum?) O pleno emprego para o futuro imediato.
Talvez a característica mais interessante e provocativa do que temos feito é que partimos de um pressuposto em que os graus de liberdade correspondentes a uma determinada região do espaço são descritos por um espaço dimensional-finito de Hilbert. Em certo sentido, isso é natural, tal como resulta da fronteira de Bekenstein (à entropia total que pode caber em uma região) ou o princípio holográfico (que limita os graus de liberdade pela área do limite de sua região). Mas, por outro lado, é completamente contrário ao que estamos habituados a pensar a partir da teoria quântica de campos, que geralmente assume que o número de graus de liberdade em qualquer região do espaço é infinitamente grande, correspondendo a um espaço de Hilbert de dimensão infinita. (Por si só isso não é algo tão preocupante, um único oscilador harmônico simples é descrito por um espaço dimensional-infinito de Hilbert, apenas porque a sua energia pode ser arbitrariamente grande). As pessoas gostam dos argumentos de Jacobson e Seth Lloyd onde, por motivos muito gerais, qualquer teoria com a gravidade irá ser localmente descrita por espaços de Hilbert de dimensão finita.
Essa é uma grande cartada, se for verdade, e eu não acho que os físicos têm realmente absorvido as consequências da ideia ainda. A teoria de campos é incorporada na forma como pensamos sobre o mundo; todas as infinidades notórias da física de partículas que nós trabalhamos tão duro para renormalizar sua distância devem sua existência ao fato de que há um número infinito de graus de liberdade. Um espaço de dimensão finita de Hilbert descreve um mundo muito diferente. Em muitos aspectos, é um mundo muito mais simples – um que deve ser mais fácil de entender. O que devemos ver.
Parte de mim acha que a imagem ao longo destas linhas – Geometria emergente de informação quântica, obedecendo a uma versão da equação de Einstein no limite clássico – praticamente tem que ser verdade, se você acredita que (1) regiões do espaço tem um número finito de graus de liberdade, e (2) o mundo é descrito por uma função de onda no espaço de Hilbert. Estes são postulados bastante razoáveis, por si mesmos, mas é claro que pode haver qualquer número de voltas e mais voltas para chegar onde queremos ir, se é que isto é possível. Pessoalmente acho que as perspectivas são empolgantes, e estou ansioso para ver onde essas ideias nos levarão.