Por Natalie Wolchover
Publicado na Quanta Magazine
Na década de 1960, o carismático físico Geoffrey Chew adotou uma visão radical do universo, e com ele, uma nova maneira de fazer física. Os teóricos da época estavam lutando para encontrar ordem em um zoológico desordenado de partículas recém-descobertas. Eles queriam saber quais eram os blocos fundamentais da natureza e quais eram os compostos. Mas Chew, professor da Universidade da Califórnia em Berkeley, argumentou contra tal distinção. “A natureza é como ela é porque esta é a única natureza possível consistente consigo mesma”, escreveu na época. Ele acreditava que podia deduzir as leis da natureza unicamente a partir da exigência de serem autoconsistentes.
Cientistas desde que Demócrito tomaram uma abordagem reducionista para entender o universo, vendo tudo nele como sendo construído a partir de algum tipo de material fundamental que não pode ser mais explicado. Mas a visão de Chew de um universo autodeterminante exigia que todas as partículas fossem igualmente compostas e fundamentais. Ele conjeturou que cada partícula é composta de outras partículas, e os outros são mantidos juntos trocando a primeira partícula em um processo que transmite uma força. Assim, as propriedades das partículas são geradas por ciclos de realimentação auto-consistentes.
A abordagem de Chew, conhecida como filosofia bootstrap, método bootstrap, ou simplesmente “bootstrap”, veio sem um manual de operação. O objetivo era aplicar quaisquer princípios gerais e condições de coerência que estivessem à mão para inferir o que as propriedades das partículas (e, portanto, toda a natureza) simplesmente tinham que ser. Um triunfo precoce no qual os alunos de Chew usaram o bootstrap para prever a massa do méson rho – uma partícula feita de pions que são mantidos juntos por troca de mésons rho – ganhou muitos adeptos.
Mas o méson rho acabou por ser um caso especial, e o método bootstrap logo perdeu impulso. Uma teoria concorrente lançou partículas como prótons e nêutrons como compostos de partículas fundamentais chamados quarks. Esta teoria das interações de quarks, chamada cromodinâmica quântica, melhorou os dados experimentais e logo se tornou um dos três pilares do modelo padrão reinante da física de partículas.
Mas as propriedades dos quarks individuais pareciam arbitrárias, e em outro universo poderiam ter sido diferentes. Os físicos foram forçados a reconhecer que o conjunto de partículas que passam a povoar o universo não refletem a única teoria consistente possível da natureza. Em vez disso, uma interminável variedade de possíveis partículas podem ser imaginadas interagindo em qualquer número de dimensões espaciais, cada situação descrita por sua própria “teoria do campo quântico”.

O bootstrap enfraqueceu por décadas esquecido pela física. Mas recentemente o campo foi re-energizado quando físicos descobriram novas técnicas de bootstrap que parecem resolver muitos problemas. Embora as condições de consistência ainda não sejam de grande ajuda para classificar as complicadas dinâmicas de partículas nucleares, o bootstrap está se revelando uma ferramenta poderosa para a compreensão de teorias mais simétricas e perfeitas que, de acordo com especialistas, servem como “sinalizadores” ou “blocos de construção” no espaço de todas as possíveis teorias quânticas de campo.
À medida que a nova geração de bootstrappers explora este espaço de teoria abstrata, eles parecem estar verificando a visão que Chew, agora com 92 anos de idade e aposentado, estabeleceu há meio século – mas eles estão fazendo isso de uma maneira inesperada. Suas descobertas indicam que o conjunto de todas as teorias de campo quânticas forma uma estrutura matemática única, que de fato origina seus próprios bootstraps, o que significa que pode ser entendido em seus próprios termos.
À medida que os físicos usam o bootstrap para explorar a geometria desse espaço teórico, eles estão apontando as raízes da “universalidade”, fenômeno notável no qual comportamentos idênticos surgem em materiais muito diferentes, como ímãs e água. Eles também estão descobrindo características gerais das teorias da gravidade quântica, com aparentes implicações para a origem quântica da gravidade em nosso próprio universo e a origem do espaço-tempo em si. Como os principais praticantes David Poland, da Universidade de Yale, e David Simmons-Duffin, do Instituto de Estudos Avançados em Princeton, Nova Jersey, escreveram em um artigo recente: “É um momento emocionante para fazer bootstrap”.
Evidenciando o Bootstrap
O bootstrap é tecnicamente um método para calcular “funções de correlação” – fórmulas que codificam as relações entre as partículas descritas por uma teoria quântica de campo. Considere um pedaço de ferro. As funções de correlação deste sistema expressam a probabilidade de que os átomos de ferro sejam magneticamente orientados na mesma direção, como uma função das distâncias entre eles. A função de correlação de dois pontos dá a probabilidade de que dois átomos estejam alinhados, a função de correlação de três pontos codifica as correlações entre quaisquer três átomos, e assim por diante. Essas funções dizem essencialmente tudo sobre o pedaço de ferro. Mas eles envolvem infinitamente muitos termos crivados com expoentes e coeficientes desconhecidos. Eles são, em geral, onerosos para calcular. A abordagem bootstrap tenta restringir o que os termos das funções podem possivelmente ser na esperança de resolver as variáveis desconhecidas. Na maioria das vezes, isso não te leva longe. Mas em casos especiais, como o físico teórico Alexander Polyakov começou a descobrir em 1970, o bootstrap leva você por todo o caminho.
Polyakov, então no Instituto Landau de Física Teórica na Rússia, foi atraído para esses casos especiais pelo mistério da universalidade. Como os físicos da matéria condensada estavam apenas descobrindo, quando materiais que são completamente diferentes no nível microscópico estão sintonizados com os pontos críticos em que eles sofrem transições de fase, eles de repente exibem os mesmos comportamentos e podem ser descritos pelo exato mesmo punhado de números. O ferro aquecido à temperatura crítica, onde se magnetiza, por exemplo, e as correlações entre seus átomos, são definidas pelos mesmos “expoentes críticos” que caracterizam a água no ponto crítico onde suas fases de líquido e vapor se encontram. Esses expoentes críticos são claramente independentes dos detalhes microscópicos de cada material, surgindo de algo que ambos os sistemas, e outros, em sua “classe de universalidade”, têm em comum. Polyakov e outros pesquisadores queriam encontrar as leis universais que conectam esses sistemas. “E o objetivo, o santo graal de tudo isso, eram esses números”, disse ele. Os pesquisadores queriam ser capazes de calcular os expoentes críticos do zero.
O que os materiais em pontos críticos têm em comum, percebeu Polyakov, são suas simetrias: o conjunto de transformações geométricas que deixam esses sistemas inalterados. Ele conjeturou que materiais críticos respeitam um grupo de simetrias chamado “simetrias conformes”, incluindo, mais importante, a simetria de escala. Aproximando ou afastando o ferro em seu ponto crítico, você sempre verá o mesmo padrão: arranjos de átomos orientados ao norte apontando para cima estão cercados por arranjos de átomos apontando para baixo; estes, por sua vez estão dentro de arranjos maiores de átomos voltados para cima, e assim por diante em todas as escalas de ampliação. Simetria de escala significa que não há noções absolutas de “próximo” e “longe” em sistemas conformes; se você inverter um dos átomos de ferro, o efeito é sentido em toda parte. “A coisa toda é organizada em um meio fortemente correlacionado”, explicou Polyakov.
O mundo em geral não é obviamente conformal. A existência de quarks e outras partículas elementares “quebra” a simetria de escala, introduzindo a massa fundamental e as escalas de distância, contra as quais outras massas e comprimentos podem ser medidos. Consequentemente, planetas, compostos por hordas de partículas, são muito mais pesados e maiores do que nós, e somos muito maiores do que átomos, que são gigantes comparados aos quarks. A quebra de simetria torna a natureza hierárquica e injeta variáveis arbitrárias em suas funções de correlação – as qualidades que prejudicaram o método de bootstrap de Chew e todo seu potencial.

Mas os sistemas conformais, descritos por “teorias de campos conformes” (CFTs), são uniformes tanto para cima quanto para baixo, e isso, descobriu Polyakov, torna altamente acessível a uma abordagem bootstrap. Em um ímã em seu ponto crítico, por exemplo, a simetria de escala restringe a função de correlação de dois pontos, exigindo que ela fique a mesma quando você redimensiona a distância entre os dois pontos. Outra simetria conformal diz que a função de três pontos não deve mudar quando você inverte as três distâncias envolvidas. Alexander Belavin, Polyakov e Alexander Zamolodchikov mostraram que há um número infinito de simetrias conformes em duas dimensões espaciais que poderiam ser usadas para restringir as funções de correlação das teorias de campo conformal bidimensional. Os autores exploraram essas simetrias para resolver os expoentes críticos de um famoso CFT chamado modelo 2-D Ising – essencialmente a teoria de um ímã plano. O “bootstrap conformal”, o procedimento personalizado da BPZ para explorar simetrias conformes, atingiu a fama.
Contudo, muito menos simetrias conformes existem em três dimensões ou mais. Polyakov poderia escrever uma “equação bootstrap” para 3-D CFTs – essencialmente, uma equação dizendo que uma maneira de escrever a função de quatro correlações de, digamos, um ímã real, deve ser igual a outro – mas a equação era muito difícil de resolver.
“Eu basicamente comecei a fazer outras coisas”, disse Polyakov, que passou a fazer seminários sobre a teoria das cordas e é agora professor na Universidade de Princeton. O bootstrap conforme, como o bootstrap original mais de uma década antes, caiu em desuso. A calmaria durou até 2008, quando um grupo de pesquisadores descobriu um poderoso truque para aproximar as soluções da equação de bootstrap de Polyakov para CFTs com três ou mais dimensões. “Francamente, eu não esperava isso, e eu pensei originalmente que havia algum erro lá”, disse Polyakov. “Pareceu-me que a informação colocada nas equações era muito pequena para obter tais resultados”.
Torções surpresas
Em 2008, o Large Hadron Collider estava prestes a começar a procurar o bóson de Higgs, uma partícula elementar cujo campo associado dá massa às outras partículas. Os teóricos Riccardo Rattazzi na Suíça, Vyacheslav Rychkov na Itália, e seus colaboradores, queriam ver se poderia haver uma teoria do campo conformal que fosse responsável pela distribuição de massa em vez do Higgs. Eles escreveram uma equação bootstrap que tal teoria teria que satisfazer. Como essa era uma teoria de campo conformal de quatro dimensões, descrevendo um campo quântico hipotético em um universo com quatro dimensões de espaço-tempo, a equação de bootstrap era muito complexa para ser resolvida. Mas os pesquisadores encontraram uma maneira de colocar limites sobre as possíveis propriedades dessa teoria. No final, eles concluíram que não existia tal CFT (e, de fato, o LHC encontrou o bóson de Higgs em 2012). Mas seu novo truque de bootstrap abriu uma mina de ouro.
O truque era traduzir as restrições na equação de bootstrap em um problema de geometria. Imagine os quatro pontos da função de correlação de quatro pontos (que codifica praticamente tudo sobre um CFT) como cantos de um retângulo; A equação bootstrap diz que se se você perturbar um sistema conformal nos cantos um e dois vai medir os efeitos nos cantos três e quatro, ou se perturbar o sistema em um e três medirá em dois e quatro, e a mesma função de correlação se mantém em ambos os casos . Ambas as formas de escrever a função envolvem séries infinitas de termos; sua equivalência significa que a primeira série infinita menos a segunda é igual a zero. Para descobrir quais termos satisfazem essa restrição, Rattazzi, Rychkov e companhia invocaram outra condição de consistência chamada “unitaridade”, que exige que todos os termos da equação tenham coeficientes positivos. Isso lhes permitiu tratar os termos como vetores, ou flechas pequenas que se estendem em um número infinito de direções a partir de um ponto central. E se um plano pudesse ser encontrado de tal forma que, em um subconjunto finito de dimensões, todos os vetores apontam para um lado do plano, então há um desequilíbrio; este conjunto particular de termos não pode somar a zero, e não representa uma solução para a equação de bootstrap.
Os físicos desenvolveram algoritmos que lhes permitiram pesquisar tais planos e uniram o espaço de CFTs viáveis a uma precisão extremamente alta. A versão mais simples do procedimento gera “parcelas de exclusão” onde duas curvas se encontram em um ponto conhecido como “torção”. As parcelas descartam CFTs com expoentes críticos que ficam fora da área delimitada pelas curvas.
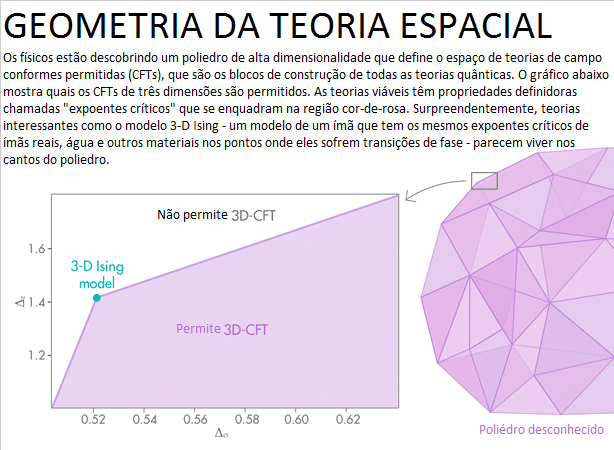
Surpreendentes características destas parcelas surgiram. Em 2012, os pesquisadores usaram o truque de Rattazzi e Rychkov para descrever os valores dos expoentes críticos do modelo 3-D Ising, um CFT notoriamente complexo que está na mesma classe de universalidade que ímãs reais, água, misturas líquidas e muitos outros materiais em seus pontos críticos. Em 2016, Poland e Simmons-Duffin calcularam os dois principais expoentes críticos da teoria até suas milionésimas casas decimais. Mas ainda mais impressionante do que este nível de precisão é onde o modelo 3-D Ising caiu entre todas as possibilidades do 3-D CFTs. Seus expoentes críticos poderiam ter caído em qualquer lugar na região permitida no gráfico de exclusão 3-D CFT, mas inesperadamente, os valores pousaram exatamente na torção no gráfico. Os expoentes críticos correspondentes a outras classes de universalidade bem conhecidas encontram-se nas torções em outras parcelas de exclusão. De alguma forma, cálculos genéricos estavam apontando teorias importantes que aparecem no mundo real.
A descoberta foi tão inesperada que Polyakov inicialmente não acreditou. Sua suspeita, compartilhada por outros, era que “talvez isso aconteceu porque há alguma simetria oculta que ainda não encontramos”.
“Todo mundo está animado porque essas torções são inesperadas e interessantes, e elas te dizem onde vivem as teorias interessantes”, disse Nima Arkani-Hamed, professora de física do Institute for Advanced Study. “Poderia estar refletindo uma estrutura poliédrica do espaço de teorias de campo conformes permitidas, com teorias interessantes que não vivem no interior ou em algum lugar aleatório, mas vivem nos cantos”. Outros pesquisadores concordaram que isso é o que as coisas sugerem. Arkani-Hamed especula que o poliedro está relacionado com o “amplituedro”, ou poderia até englobar um objeto geométrico que ela e um colaborador descobriram em 2013, que codifica as probabilidades de diferentes resultados de colisão de partículas – exemplos específicos de funções de correlação.
Os pesquisadores estão atirando para todos os lados. Alguns estão aplicando o bootstrap para ter uma luz sobre uma teoria de campo “superconformal” especialmente simétrica conhecida como teoria (2.0), que desempenha um papel na teoria das cordas e é conjecturada para existir em seis dimensões. Mas Simmons-Duffin explicou que o esforço para explorar CFTs levará os físicos além destas teorias especiais. Teorias quânticas de campo mais gerais como a cromodinâmica quântica podem ser derivadas começando com um CFT e “fluindo” suas propriedades usando um procedimento matemático chamado de grupo de renormalização. “Os CFTs são parecidos com sinais na paisagem das teorias quânticas de campo, e os fluxos de grupos de renormalização são como as estradas”, disse Simmons-Duffin. “Então você tem que primeiro entender os sinais, e então você pode tentar descrever as estradas entre eles, e dessa forma você pode fazer um mapa do espaço das teorias.”
Tom Hartman, um bootstrapper da Universidade de Cornell, disse que mapear o espaço das teorias de campo quântico é o “grande objetivo do programa bootstrap”. As parcelas CFT, disse ele, “são uma versão muito difusa desse mapa final”.
Descobrir a estrutura poliédrica representando todas as possíveis teorias de campo quânticas iria, em certo sentido, unificar interações de quarks, ímãs e todos os fenômenos observados e imaginados em uma única e inevitável estrutura – uma espécie de versão atualizada da frase de Geoffrey Chew “única natureza possível consistente consigo mesma”. Mas, como Hartman, Simmons-Duffin e dezenas de outros pesquisadores do mundo buscam essa abstração, eles também estão usando o bootstrap para explorar uma conexão direta entre os CFTs e as teorias que muitos físicos adoram. “Explorar possíveis teorias de campos conformes também significa explorar possíveis teorias da gravidade quântica”, disse Hartman.
Gravidade Quântica do Bootstrap
O bootstrap conformal está se tornando uma ferramenta poderosa para a pesquisa da gravidade quântica. Em um artigo de 1997 que agora é um dos mais citados na história da física, o teórico argentino-americano Juan Maldacena demonstrou uma equivalência matemática entre um CFT e um ambiente gravitacional do espaço-tempo com pelo menos uma dimensão espacial extra. A dualidade de Maldacena, chamada “correspondência AdS/CFT”, ligava o CFT a um correspondente “espaço anti-de Sitter”, que, com sua dimensão extra, sai do sistema conformal como um holograma. O espaço AdS tem uma geometria olho-de-peixe diferente da geometria do espaço-tempo do nosso universo, e ainda assim a gravidade funciona da mesma maneira que aqui. Ambas as geometrias, por exemplo, dão origem a buracos negros – objetos paradoxais que são tão densos que nada dentro deles pode escapar de sua gravidade.
As teorias existentes não se aplicam dentro de buracos negros; se você tentar combinar a teoria quântica com a teoria da gravidade de Albert Einstein (que lança gravidade como curvas no tecido espaço-tempo), surgem paradoxos. Uma questão importante é como os buracos negros conseguem preservar a informação quântica, mesmo quando a teoria de Einstein diz que elas evaporam. Resolver esse paradoxo exige que os físicos encontrem uma teoria quântica da gravidade – um conceito mais fundamental a partir do qual o espaço-tempo emerge em baixas energias, como fora buracos negros. “A coisa surpreendente sobre AdS/CFT é que ele dá um exemplo funcional de gravidade quântica onde tudo é bem definido e tudo o que temos a fazer é estudá-lo e encontrar respostas para esses paradoxos”, disse Simmons-Duffin.
Se a correspondência AdS/CFT fornece aos físicos teóricos um microscópio para as teorias de gravidade quântica, o bootstrap conformal lhes permitiu ligar a luz do microscópio. Em 2009, os teóricos usaram o bootstrap para encontrar evidências de que cada CFT conheça certas condições se aproximando de uma teoria gravitacional dupla no espaço AdS. Desde então, eles estão elaborando um dicionário preciso para traduzir expoentes críticos e outras propriedades de CFTs e características equivalentes do holograma do espaço AdS.
Durante o ano passado, bootstrappers como Hartman e Jared Kaplan da Universidade Johns Hopkins fizeram rápidos progressos no entendimento de como os buracos negros funcionam nesses universos olho-de-peixe e, em particular, como a informação é preservada durante a evaporação do buraco negro. Isso poderia afetar significativamente a compreensão da natureza quântica da gravidade e do espaço-tempo em nosso próprio universo. “Se eu tiver algum pequeno buraco negro, não importa se ele está no espaço AdS; é pequeno em comparação com o tamanho da curvatura”, explicou Kaplan. “Se você puder resolver essas questões conceituais no espaço AdS, então parece muito plausível que a mesma resolução se aplique na cosmologia”.
Não está claro se o nosso próprio universo surge de forma holográfica de uma teoria de campo conformal da maneira como os universos do AdS fazem, ou se esta é realmente a maneira correta de se pensar sobre isso. A esperança é que, ao fazer o bootstrap do caminho em torno da estrutura geométrica unificadora de possíveis realidades físicas, os físicos terão uma melhor ideia de onde nosso universo se encaixa no grande esquema das coisas – e qual é esse grande esquema. Polyakov está impulsionado pelas recentes descobertas sobre a geometria do espaço teórico. “Há muitos milagres acontecendo”, disse ele. – E, provavelmente, saberemos o por quê.