Por Por Joe Garland
Publicado na From Quarks to Quasars
Independentemente da sua formação científica (ou falta dela), a 4ª dimensão é um conceito muito difícil de entender. Para entender o quão difícil é imaginar um mundo com uma 4ª dimensão espacial, vamos usar algumas comparações. Primeiro, imagine uma cor que não existe atualmente. Em seguida, tente chegar a uma maneira de explicar cores (como o azul, por exemplo) para alguém que não pode ver. Ambas as coisas são muito difíceis, não é? Bem, nos deparamos com exatamente os mesmos problemas quando tentamos imaginar uma 4ª dimensão espacial. Mesmo para aqueles de nós com as mais poderosas imaginações visuais, tentar imaginar como um objeto quadridimensional ficaria em um mundo tridimensional é impossível. Verdadeiramente e totalmente impossível.
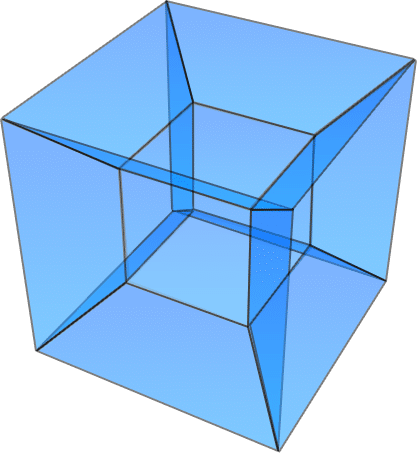
No entanto, a matemática nos oferece um pouco de ajuda nesta área. Veja, para um matemático, a 4ª dimensão pode ser representada usando geometria de coordenadas e vetores dentro de um espaço algébrico quadridimensional (isso soa estranho, mas basta olhar para a imagem para ter uma ideia do que significa). Claro, esta é apenas uma DIREÇÃO adicional escrita em um pedaço de papel em 2D e não uma dimensão real. Neste sentido, as coordenadas seriam tratadas exatamente da mesma forma que as outras três direções, para que ela realmente não acrescente nada de novo ao nosso entendimento. As coordenadas geométricas ainda ajudam-nos a compreender o quão difícil é para os seres que vivem em um mundo tridimensional (como nós) entender a quarta dimensão.
Mesmo assim, compreender um mundo com quatro dimensões espaciais ainda é extremamente difícil. Mas que graça teria se não tentássemos?
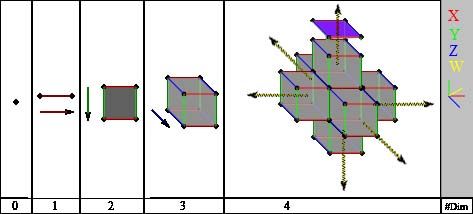
O método de explicação mais simples:
Uma das maneiras mais eficazes de explicar esta dimensão indescritível é a utilização de uma sequência de hipercubos, a partir da dimensão zero levando até a 4ª dimensão (assim serão cinco dimensões separadas no geral). Nosso primeiro hipercubo (vamos chama-lo de “HC” para abreviar) é o 0-HC – que ocupa nenhum volume, pois não tem largura, comprimento nem profundidade. Ele é, efetivamente, um ponto infinitamente pequeno no espaço. Esta ideia é muito usada em física e matemática para simplificar cenários e desenvolver equações. Por exemplo, quando usando as leis de Newton para criar uma equação para a pressão de um gás em um recipiente, assume-se que as partículas não tenham volume. Você também usou esse princípio ao aprender a geometria mais básica em matemática. Ao traçar uma coordenada, antes de juntá-la a qualquer outra, você criou (em teoria) um ponto infinitamente pequeno na dimensão zero (claro, o seu lápis nunca poderia ser apontado o suficiente para literalmente fazer isso).
Em seguida, pegue o seu ponto infinitamente pequeno e estenda-o em uma única linha reta em qualquer direção – agora você criou um 1-HC. A dimensão ainda não tem largura ou altura, mas quando você deu o comprimento, o colocou na primeira dimensão. Em teoria, se você desenhar sua nova linha em uma direção infinita, você realmente vai criar toda uma 1ª dimensão – tente fazer isso em seu livro de matemática!
Após isso, pegue o 1-HC e o estenda novamente. Desta vez, estenda-o perpendicularmente à sua direção original para criar um plano (vamos fingir que você fez um quadrado). Este novo hipercubo está agora na segunda dimensão, porque é capaz de diferir em duas medições – largura e comprimento. Podemos chamá-lo de 2-HC, e da mesma forma para a sua linha 1-HC, se você expandir o quadrado infinitamente, você criaria um espaço bidimensional.
Qual é a única direção que falta para expandir nosso hipercubo? – altura. Você não pode fazer isso no papel, é claro, mas se você tiver acesso a alguns softwares gráficos 3-D de computador (o “Autograph” é bom), você pode experimentar. Para isso, você deve gerar seu 2-HC e, em seguida, levantá-lo para a 3ª dimensão criando um cubo. A nova forma tem a capacidade de ter as medidas em largura, comprimento e altura – mas todos os seus ângulos têm 90 graus. Mais uma vez, ele também pode ser expandido infinitamente para fazer todo um espaço tridimensional, e essa é, obviamente, a dimensão em que nós, humanos, vivemos.
Imaginando uma 4ª direção:
Certo, e agora? Bem, agora eu peço que você pare e tente imaginar uma 4ª direção e vá para lá por alguns segundos… Não pode fazer isso? Não temos mais sentidos na 3ª dimensão para podermos expandir nosso hipercubo (obviamente), mas isso pode ser feito na 4ª dimensão do espaço-tempo. Nós chamamos isso de tesserato. Existem várias maneiras de tentar dar uma perspectiva sobre como visualizar essa expansão, mas seria muito difícil de explicar neste artigo. Então, ao invés disso, vou tomar uma abordagem prática (dito isso, é interessante refletir sobre esta quarta expansão, e há alguns bons gráficos na web para você procurar).
Agora, então, imagine-se olhando para um pedaço de papel, e este pedaço de papel é o lar de um mundo que só existe no espaço-tempo bidimensional. Mesmo que a 2ª dimensão exista dentro da 3ª dimensão, esses seres não têm ideia de que você existe, porque eles não têm a compreensão de um outro sentido de espaço (eles não podem olhar para cima para ver você, porque esse não é um conceito que eles possam sondar) . É fácil para nós dizer “altura”, porque nós experimentamos altura – lembra-se como era difícil para você pensar em uma 4ª direção? Se você cutucar o mundo deles com seu dedo, ele pareceria como um disco sem altura (possivelmente sem cor) quando visto de lado. Além disso, se eles estavam do lado de fora de um quadrado com um ponto dentro, você poderia facilmente chegar dentro desse quadrado e retirar o ponto. Os seres bidimensionais não teriam nenhuma ideia de como isso foi possível, porque para eles, você apenas de alguma forma passou pelos os únicos limites dimensionais conhecidos por eles. Você seria capaz de fazer isso, porque a segunda dimensão tem uma secção transversal através do nosso espaço.
Eu sei que isso pode ser um pouco confuso, mas é útil para imaginar como um ser que exista na 4ª dimensão se parece para nós. Nós não poderíamos dizer muito ao certo como eles iriam parecer, mas me disseram uma vez que seriam parecidos com “um monte de manchas de pele”. A criatura quadridimensional seria capaz de ver tudo em nosso espaço tridimensional porque ela existiria fora das nossas fronteiras – podendo ver dentro de qualquer objeto. Isso seria horrível, mas eles teriam o poder de ver dentro de seu corpo e remover qualquer um dos seus órgãos, sem nunca ter que penetrar sua pele. Assim como você pode remover o ponto, puxando-o em sua dimensão, eles podem fazer o mesmo com você (possivelmente algum tipo de vingança em uma aliança bidimensional/quadridimensional?). Da mesma forma, essas criaturas podem muito bem existir em nosso próprio universo sem serem detectadas, mas, novamente, nunca seríamos capazes de vê-las, assim como os seres bidimensionais nunca poderiam nos ver.
Ok. É uma coisa MUITO louca para se refletir.
