Por Rishabh Nakra
Publicado no The Secrets Of The Universe
Significado da equação: Se a massa de uma anã branca exceder 1,4 massa solar, ela entrará em colapso sob sua própria gravidade. Assim, 1,4 massa solar é a massa máxima de uma estrela anã branca estável.
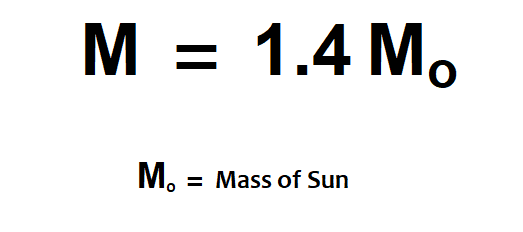
Fazem quase 109 anos desde o nascimento de Subrahmanyan Chandrasekhar e, por isso, decidi dedicar a equação de hoje a essa lenda. Hoje, vou esclarecer a famosa equação que leva seu nome, o limite de Chandrasekhar. Esse artigo também lhe dará um vislumbre da importância da mecânica estatística na astrofísica. Como de costume, vamos começar do zero.
Para chegar ao limite de Chandrasekhar, primeiro precisamos responder a duas importantes questões: Como as estrelas evoluem e como o Princípio de Exclusão de Pauli “salva” a estrela. Começaremos com a primeira pergunta: Como as estrelas evoluem? Vou explicar da forma mais simples e breve possível.
Uma estrela é uma bola quente de plasma. Existe uma região central na estrela que abriga a reação de fusão nuclear. Uma estrela gasta 90% da sua vida fundindo a reação mais básica de fusão nuclear: hidrogênio em hélio em seu centro. Essa estrela é conhecida como a estrela de sequência principal, um exemplo é o nosso Sol. A principal característica dessa estrela é estar em perfeito equilíbrio hidrostático. Está ficando difícil? Considere isso: A estrela é massiva. Tão massiva que começa a colapsar sobre sua própria gravidade. Mas o que impede o colapso gravitacional interno é a pressão externa (gás) da reação nuclear central. Assim, o colapso gravitacional para dentro é perfeitamente balanceado pela pressão externa do gás e a estrela é considerada em equilíbrio hidrostático.
Quando todo o hidrogênio é convertido em hélio, o próximo elemento da cadeia, carbono, se forma. A temperatura requerida para a fusão de hidrogênio em hélio foi de cerca de 15 milhões K e para fusão de hélio ao carbono necessita em torno de 100 milhões K. Um dia, novamente, todo o hélio funde em carbono e o que sobra é um núcleo de carbono inerte. A temperatura necessária para fundir o carbono é próximo de 500 milhões K. As estrelas de porte pequeno a médio não têm o potencial de suportar uma fusão de carbono em grande escala. Isso é tudo o que precisamos saber sobre evolução estelar para entender o limite de Chandrasekhar. Passamos agora para a próxima pergunta.
Agora, na ausência da reação principal, a gravidade ganha vantagem e começa a colapsar a estrela. Esse colapso começa a aumentar a densidade da região central. Assim, a separação média entre as partículas constituintes diminui e se torna da ordem do comprimento de onda de-Broglie (ignore esse conceito de comprimento de onda se ficar difícil de entender. Apenas saiba que a densidade aumenta e a separação p/w diminui). Tal sistema de alta densidade é conhecido como sistema degenerado. Agora, quem salvará a estrela?
A resposta: elétrons! Essas pequenas partículas subatômicas odeiam ser esmagadas. Elas são férmions e obedecem ao princípio de exclusão de Pauli. Assim, não mais que dois elétrons (um com spin up e outro com spin down) podem ocupar o mesmo estado quântico. Desse modo, à medida que a gravidade tenta esmagar a estrela, todos os estados de energia inferior disponíveis começam a ser preenchidos. Agora, como outros elétrons não podem ocupar os estados de energia inferior já preenchidos, eles precisam preencher os estados de energia mais elevados. Os elétrons do estado de energia inferior dirão: “Não! Você não pode ocupar esse estado. Nós já o ocupamos. Você precisa ir para níveis de energia mais altos. Vamos exercer uma pressão externa se você tentar ocupar esse estado”. Essa pressão é conhecida como pressão de degenerescência eletrônica. Assim, em um sistema altamente degenerado, os elétrons com os mais altos estados de energia têm a incrível quantidade de velocidade associada a eles (porque estão em níveis de energia mais altos e, portanto, a energia cinética é maior). Tão maior que agora os efeitos relativísticos entram em cena. (Para matemática completa desse conceito, veja isso).
Em uma anã branca estável, o colapso gravitacional interno é balanceado pela pressão de degenerescência eletrônica. Mas se a massa de uma estrela ficar maior do que 1,4 a do Sol, até mesmo a pressão de degenerescência eletrônica se romperá. Os elétrons se combinarão com prótons e formarão nêutrons e, assim, uma estrela de nêutrons. Esse limite de massa, abaixo do qual a estrela anã branca é estável, é conhecido como o limite de Chandrasekhar.
Veja o quão importante é a mecânica estatística para a astrofísica. É uma das mais importantes ferramentas com a qual um astrofísico decodifica o universo.