Dando continuidade ao assunto tratado no post anterior, iremos falar sobre a evolução da sistematização das Leis do Pensamento (LdP) e da Lógica de modo geral, além de abordar a forma como a disciplina interagiu com a matemática a partir da Era Moderna até o final do século XIX.
A contribuição de Leibniz
O filósofo e matemático Gottfried Leibniz (1646 -1716) trouxe avanços significativos para o campo da Lógica e introduziu a ideia de que o pensamento humano pode ser reduzido a cálculos e fórmulas [1]. Em diversas das suas obras, Leibniz invocou ao menos sete princípios filosóficos, sendo que dois desses princípios coincidem com as LdP. O Princípio da Identidade seria análogo à Lei da Não-contradição e à Lei da Identidade. Já o Princípio da Identidade dos Indiscerníveis* pode ser entendido como uma derivação das LdP, embora exista a discussão se esse princípio é lógico ou ontológico [2].

Leibniz era apaixonado por símbolos e pode-se dizer que foi pioneiro na ideia que daria origem à moderna lógica simbólica: pensamentos poderiam ser transcritos a partir da combinação de caracteres ou símbolos. Pensamentos complexos seriam formados pela relação entre pensamentos simples, de forma análoga às relações aritiméticas. A vantagem da ideia de Leibniz é justamente facilitar o entendimento, além da detecção de erros e contradições se tornar muito mais simples (do mesmo modo que detectamos um erro em uma equação).
Outra contribuição de Leibniz foi o conceito de calculus ratiocinator , que pode ser interpretado como uma antecipação da lógica matemática, uma espécie de framework lógico para cálculos. Alguns autores entendem o ratiocinator como uma máquina (hardware) de calcular, enquanto outros defendem a interpretação de que seria como um software.
Apesar das ideias inovadoras para seu tempo, o filósofo alemão não possui nenhuma obra sobre lógica formal publicada e as informações estão dispersas em cartas e manuscritos. Existe, no entanto, um debate se Leibniz influenciou o desenvolvimento da lógica no século XIX ou se ele antecipou os seus princípios básicos [3].
A era de ouro da lógica

É praticamente impossível falar de LdP sem mencionar o trabalho de George Boole (1815-1864). O matemático inglês revolucionou a lógica com as suas obras Mathematical Analysis of Logic (Análise Matemática da Lógica), publicada em 1847, e An Investigation of the Laws of Thought (Uma investigação das Leis do Pensamento, em português), publicada em 1854. Boole propôs a representação simbólica das proposições lógicas aristotélicas por meio de uma abordagem algébrica.
A partir da lógica booleana, proposições e princípios puderam ser escritos em termos de verdadeiro (1) ou falso (0) e as operações lógicas, assim como suas propriedades, são expressas a partir de fórmulas e símbolos.
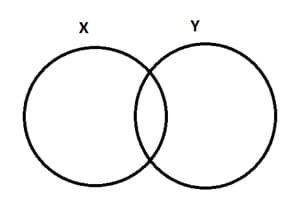
Os três operadores básicos são conjunção (E,AND, ˄); disjunção (OU, OR, ˅) e negação (NÃO,NOT, ¬). Eles são geralmente representados como se fossem fruto da relação entre conjuntos matemáticos: por exemplo, tem-se dois conjuntos, X e Y:
A parte destacada em laranja no esquema abaixo representa as relações de interseção, união e negação entre os conjuntos e o universo em que estão inseridos:
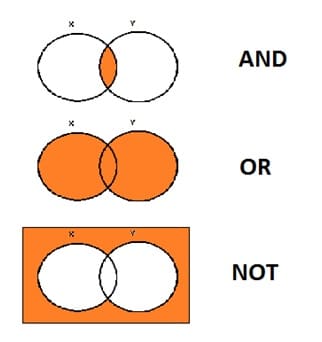
Pode parecer simplório, mas esse sistema permite representar de modo claro leis e princípios fundamentais da lógica. Por exemplo, a Lei da Não-contradição pode ser expressa na forma: X ˄¬X= {} (X e não-X é igual a conjunto vazio, ou seja, não “existe”), já a Lei do Terceiro Excluído seria X˅¬X =1.
A álgebra de Boole também apresenta, a partir dos seus postulados, algumas propriedades representadas na tabela abaixo:

A lógica booleana é não só uma das maiores contribuições para a lógica matemática, mas também se tornou essencial para a computação que surgiu décadas depois: computadores, máquinas de calcular e diversos aparelhos eletrônicos que usamos no dia-a-dia operam segundo essa lógica , por meio do código binário (1s e 0s). Infelizmente, não podemos nos aprofundar muito no assunto, mas existe um vasto material disponível em livros e artigos online para aqueles que tiverem interesse. [4]
Além de George Boole, outro inglês deu uma importante contribuição aos estudos de Lógica: Charles Dodgson (1832-1898), mais conhecido pelo pseudônimo Lewis Carroll. Isso mesmo, é o autor de Alice no País das Maravilhas e Alice Através do Espelho. Dodgson, além de escritor, era matemático e lencionava a disciplina no colégio local.

Carroll não se limitou a obras literárias, mesmo estas sendo recheadas de referências à lógica e à matemática, e escreveu trabalhos não-literários significativos na área: The Game of Logic (O jogo da Lógica), publicado em 1887, e Symbolic Logic (Lógica Simbólica), publicado postumamente, apresentam diversos conceitos que seriam utilizados por lógicos modernos posteriormente, como o conceito de classe (class, set), diferentia. Além disso, os livros contém jogos, enigmas e quebra-cabeças, que estimulavam o raciocínio sistemático de modo divertido e despretensioso, o que contribuiu para a popularização do tema. Nas palavras do próprio autor:
“Once master the machinery of Symbolic Logic, and you have a mental occupation always at hand, of absorbing interest, and one that will be of real use to you in any subject you may take up. It will give you clearness of thought – the ability to see your way through a puzzle – the habit of arranging your ideas in an orderly and get-at-able form – and, more valuable than all, the power to detect fallacies, and to tear to pieces the flimsy illogical arguments, which you will so continually encounter in books, in newspapers, in speeches, and even in sermons, and which so easily delude those who have never taken the trouble to master this fascinating Art.” (CARROLL, Lewis) [5]
“Uma vez dominada a maquinaria da Lógica Simbólica, e você tem uma ocupação mental sempre à mão, de interesse envolvente, e um que irá ser de real uso a você em qualquer assunto que você escolha. Lhe dará clareza de pensamento – a habilidade de resolver um quebra-cabeça – o hábito de organizar as suas ideias em uma forma ordenada e fácil de entender – e, mais importante de todos, o poder de detectar falácias, e reduzir a pó argumentos ilógicos e inconsistentes, que você irá encontrar continuamente em livros, jornais, discursos, e até em sermões, e que tão facilmente iludem aqueles que nunca se deram ao trabalho de dominar essa Arte fascinante.” (tradução nossa)
A maioria das obras de Lewis Carroll estão disponíveis gratuitamente no Projeto Gutenberg (em inglês), então para os curiosos que querem adentrar na toca do coelho carrolliano – ba dum tss – basta clicar aqui (inserir esse link https://www.gutenberg.org/ebooks/search/?query=lewis+carroll&go=Go) .
Deixando um pouco as terras britânicas (voltaremos lá em um instante), um outro importante filósofo, matemático, lógico e polímata deu volumosas contribuições para o campo da lógica em meados do século XIX: Charles Sanders Peirce (1839-1914). Americano, considerado do pai da disciplina conhecida como semiótica (estudo dos signos) e da escola pragmática, Peirce inventou dezenas de sistemas de sintaxe lógica e parte das suas ideias só seria desenvolvida anos depois por outros matemáticos/lógicos. Esses sistemas incluem uma algébra semelhante a de Boole e uma sintaxe similar à de Russell. Peirce empregou alguns operadores da lógica booleana, como a disjunção e a negação.
Na sua obra Description of a Notation for the Logic of Relatives (Descrição de uma Notação para a Lógica de Relativos, em português), publicada em 1870, Peirce inaugura uma sintaxe lógica completa para expressar relações na forma de símbolos. O filósofo também introduziu a ideia de variável, embora não tivesse utilizado este nome. Também antecipou os quantificadores universais e existenciais.

Os trabalhos de Peirce abordam ainda as três formas de inferência: dedução, indução e abdução (lembram quando tratamos sobre o assunto no post anterior?), analisando a obra de Aristóteles e relacionando essas formas com a lógica e as ciências formais/normativas. Até os dias atuais existem muitos pesquisadores nos mais diversos campos (linguística, semiótica, letras, comunicação, computação) que estuda as teorias peirceanas. No Brasil, a conhecida pesquisadora Lucia Santaella é uma das principais divulgadoras das ideias de Peirce.
Retornando à Europa, um matemático, filósofo e lógico alemão estabeleceu definitivamente a lógica matemática moderna: Gottlob Frege (1848-1925). Retomando a ideia de Leibniz de uma linguagem do pensamento, Frege desenvolveu uma notação formal para o raciocínio. Em Begriffsschrift, publicado em 1879, e Grundgesetze der Arithmetik, publicado em 1903, o matemático introduziu seu sistema de representação simbólica, capaz de expressar formalmente a estrutura dos enunciados lógicos.
Na notação de Frege, todos os termos e fórmulas denotam expressões, que incluem nomes de objetos, como “3”, e termos complexos, como “3+4” e sentenças. Termos complexos são formados a partir de “expressões incompletas”, que são basicamente funções. “3+1” seria então ( )+ ( ) e 3³ seria formado a partir da expressão incompleta ( )³ [7].O elemento que preenche os parênteses é chamado de argumento na lógica fregeana.
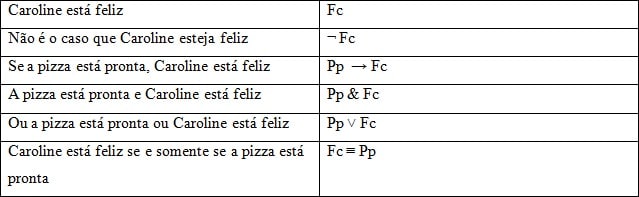
Dando um exemplo mais fácil de entender, imagine que a função F ( ) diga respeito a estar feliz e c denota Caroline, logo F (c) quer dizer: “Caroline está feliz”. O lógico alemão também analisou enunciados mais complexos, como, por exemplo, condicionais (Se…, então…). A tabela abaixo [8] ajuda a entender melhor o nosso exemplo:
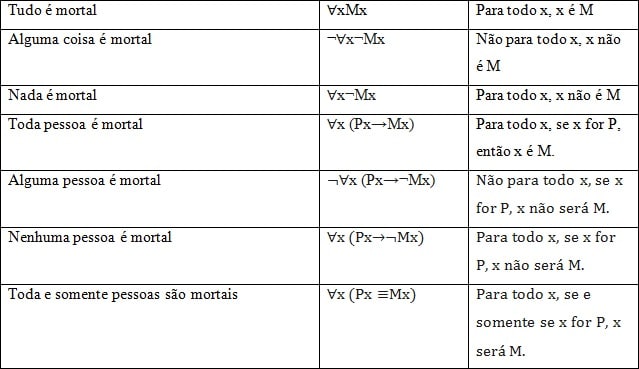
Similar ao trabalho de Russell no ensaio On denoting, Frege estabeleceu símbolos para representar quantidade, os chamados quantificadores: Tudo, Algum(a), Nada e Todo (a), Algum(a), Nenhum (a). O modo como ele representa esses enunciados quantificadores é interessante. Por exemplo, dizer “Algum” é a mesma coisa que dizer que “nem Todo x não…”. Novamente, a tabela [9] a seguir nos ajuda a visualizar melhor. Tomando-se M ( ) como a qualidade de mortal e P ( ) a qualidade de pessoa, temos:
É importante notar que o “Algum” (¬∀x¬Mx) também é representado como ∃x (existe um x). Esse quantificador é chamado de quantificador existencial, enquanto que ∀x (Todo, Tudo) é chamado de quantificador universal.
A lógica encontra seus limites?

Embora Frege tenha dado uma importante contribuição para a Lógica, suas ideias não passaram sem críticas. A mais significativa e famosa foi a do filósofo, matemático e lógico inglês Bertrand Russell (1872-1970). Russell escreveu a Frege em 1902 dizendo que havia detectado uma contradição no seu sistema, em especial na definição de função. O inglês havia observado que os predicados das funções seriam como classes ou conjuntos (set) e se imaginarmos um conjunto que engloba todos os conjuntos que não são um elemento de si, encontramos um paradoxo, uma vez que o próprio conjunto não poderia se possuir. Essa contradição ficou conhecida como Paradoxo de Russell e é explicada pelo próprio matemático neste trecho da carta a Frege:
“There is just one point where I have encountered a difficulty. You state (p. 17 [p. 23 above]) that a function too, can act as the indeterminate element. This I formerly believed, but now this view seems doubtful to me because of the following contradiction. Let w be the predicate: to be a predicate that cannot be predicated of itself. Can w be predicated of itself? From each answer its opposite follows. Therefore we must conclude that w is not a predicate. Likewise there is no class (as a totality) of those classes which, each taken as a totality, do not belong to themselves. From this I conclude that under certain circumstances a definable collection [Menge] does not form a totality.” [10]
“Existe apenas um ponto onde eu encontrei dificuldade. Você afirma (p. 17 [p. 23 acima]) que uma função também pode agir como um elemento indeterminado. Eu previamente acreditava nisso, mas agora esse ponto de vista me parece duvidoso por causa da seguinte contradição. Supondo w como predicado: ser um predicado que não pode ser predicado de si. Pode w ser predicado de si? Para cada resposta, segue-se o seu oposto. Logo, nós devemos concluir que w não é um predicado. Do mesmo modo, não existe classe (como uma totalidade) das classes que, cada uma tomada como uma totalidade, não pertencem a elas mesmas. Disso eu concluo que sob certas circunstâncias uma coleção definível não forma uma totalidade”. (tradução nossa)
Russell destruiu os sonhos de Frege, mas essa não seria a última reviravolta que a lógica sofreria naquele século. No nosso próximo artigo, trataremos de modo mais detalhado as consequências do desenvolvimento da lógica matemática no século XX e os seus limites e incompletudes.
Nota: Este artigo foi produzido baseando-se nos textos da Enciclopédia Filosófica de Standford. Trata-se, portanto, de um resumo informativo que tem por objetivo introduzir o assunto a leitores de todos os níveis de conhecimento filosófico.Não aprofundamos nenhuma das ideias aqui apresentadas, mas esperamos que este texto seja um ponto de partida para pesquisas sobre o assunto.
* Em termos leigos, o Princípio geralmente apresenta duas formas: a primeira afirma que 1. se x e y compartilham das mesmas propriedades, 2. x é igual a y. A segunda faz o “movimento inverso”: 1.se x é igual a y, então 2. x e y compartilham das mesmas propriedades. É importante salientar que a primeira forma é muito controversa, enquanto que a segunda é tida como uma verdade lógica.
REFERÊNCIAS
[1] https://en.wikipedia.org/wiki/Alphabet_of_human_thought
[2] https://en.wikipedia.org/wiki/Identity_of_indiscernibles
[3] http://plato.stanford.edu/entries/leibniz-logic-influence/
[4] http://plato.stanford.edu/entries/boole/#LawTho185
[5] http://www.math.hawaii.edu/~hile/math100/logice.htm
[6] http://plato.stanford.edu/entries/peirce/#logic
[7] http://plato.stanford.edu/entries/frege/
[8] [9] Baseadas nas tabelas do artigo http://plato.stanford.edu/entries/frege/. É importante ressaltar que não utilizamos a notação de Frege, mas a notação moderna.
[10] https://en.wikipedia.org/wiki/Russell%27s_paradox