Por Sean Carroll
Publicado no Preposterous Universe
Quantificar a gravidade é uma meta importante da física contemporânea, mas depois de décadas de esforço, isso provou ser um osso extremamente duro de roer. Então, vale a pena considerar uma mudança muito ligeira de ênfase. E se a estratégia certa não for “encontrar a teoria correta da gravidade, quantificando-a”, mas “encontrar uma teoria quântica do qual a gravidade emerge”?
Essa é uma maneira de pensar sobre uma abordagem nova e emocionante para o problema conhecido como “redes de tensores” ou “correspondência AdS/MERA”. Se você quer ter o plano de fundo e as ideias básicas apresentadas de uma forma digerível, a talentosa Jennifer Ouellette acabou de publicar um artigo no Quanta que expõe tudo isso. Se você quiser mergulhar em alguns dos âmagos da questão, meus jovens e enérgicos colaboradores e eu temos um novo paper para expor:
Condições de consistência de uma correspondência ADS/MERA
Ning Bao, ChunJun Cao, Sean M. Carroll, Aidan Chatwin-Davies, Nicholas Hunter-Jones, Jason Pollack, Grant N. Remmen.
O Multi-scale Entanglement Renormalization Ansatz (MERA) é uma rede tensora que fornece uma maneira eficiente e variada de estimar o estado fundamental de um sistema quântico crítico. A geometria da rede se assemelha a uma discretização de fatias espaciais de um espaço-tempo AdS e “geodésias” da MERA, reproduzindo a fórmula Ryu-Takayanagi para a entropia de emaranhamento de uma região de fronteira em termos de propriedades. Em consequência, foi sugerido que poderia haver uma correspondência AdS/MERA, relativo aos estados no espaço de Hilbert do sistema quântico limite para aqueles definidos na estrutura. Aqui nós investigamos esta proposta e obtemos as condições necessárias para que ela se aplique, usando características geométricas e desigualdades da entropia que esperamos manter no volume. Mostramos, talvez sem surpresa, que a rede MERA só pode descrever a física em escalas de comprimento maiores que os raios anunciados. Além disso, usando a entropia covariante ligada na maior parte, mostramos que não há parâmetros de MERA convencionais que reproduzem completamente a física em massa mesmo em escalas super-AdS. Sugerimos modificações ou generalizações deste tipo de tensor de rede que podem ser capazes de proporcionar uma correspondência mais robusta.
(E nós não somos o único grupo da Caltech pensando sobre essas coisas.)
Entre o artigo do Quanta e o nosso paper, algo deve ser basicamente explanado, mas deixe-me dar a ideia básica. Tudo começou quando teóricos da informação quântica interessados na física da matéria condensada, em particular Giufre Vidal e Glen Evenbly, estavam procurando maneiras de encontrar o estado fundamental quântico (a função de onda com menor energia possível) dos sistemas em modelos de spins (qubits) dispostos sobre uma linha. Um problema simples, mas que é muito difícil de resolver, mesmo em um computador – o espaço de Hilbert é muito grande para procurar de forma eficiente através dele. Então, eles se voltaram para a ideia de uma “rede tensora“.
Uma rede tensora é uma maneira de construir um estado complicado e altamente emaranhado de muitas partículas, começando com um estado inicial simples. O tipo particular de rede que Vidal e Evenbly se interessaram se chama MERA, Multiscale Entanglement Renormalization Ansatz (veja, por exemplo). Detalhes podem ser encontrados nos links acima; o que importa aqui é que o MERA assume a forma de uma estrutura que parece um pouco com isso.
Nosso simples ponto de partida inicial é, na verdade, o centro do diagrama. As várias ligações representam tensores que atuam no estado inicial e que fazem algo cada vez mais complicado, que culminou com o estado de muitos corpos no limite circular da imagem.
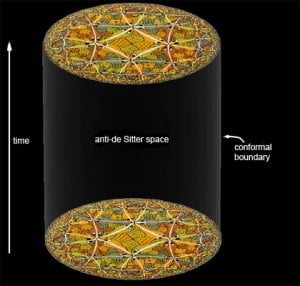
Aqui está a coisa: nada disto tinha nada a ver com a gravidade. Foi um apenas um truque calculacional bonito para encontrar estados quânticos das interações dos spins de elétrons. Mas esse tipo de imagem pode não ajudar, e sim lembrar a certos físicos teóricos um tipo muito famoso de espaço-tempo: o espaço Anti-de Sitter (AdS, sigla em inglês), a solução maximamente simétrica com a equação de Einstein, na presença de uma constante cosmológica negativa. (Ou pelo menos a parte “espacial” da mesma, que é simplesmente um plano hiperbólico).
Claro, alguém teve que ser o primeiro a realmente perceber isso, e, neste caso, foi um jovem físico chamado Brian Swingle. Brian é um físico de matéria-condensada, mas ele estava intelectualmente curioso o suficiente para fazer cursos sobre a teoria das cordas como um estudante de graduação. Lá ele aprendeu o que os teóricos das cordas amam, o AdS – é o lar natural das dualidade Gauge-gravidade de Maldacena, com uma teoria de Gauge vivendo na “fronteira” do espaço-plano e gravidade à espreita das AdS. “Volume”, Swingle se perguntou se a semelhança superficial entre a geometria da rede tensora MERA e o AdS não era realmente um sinal de algo mais profundo – seria uma correspondência AdS/MERA?
E a resposta é – talvez! Algumas das características de anúncios de gravidade são certamente capturadas pelo MERA, então tudo parece estar certo. Mas, como se diz no documento acima, com a lista extensa de autores, não apenas todos caem juntos imediatamente. Algumas coisas que você gostariam que fossem verdades no AdS não acontecem automaticamente na interpretação do MERA. Mas isso não é um assassino dele – é apenas um sinal de que temos de, pelo menos, trabalhar um pouco mais. Talvez haja uma generalização do MERA simples que devam ser consideradas, ou uma versão um pouco mais sutil da correspondência pretendida.
Vale a pena perseguir a possibilidade. Tão surpreendente (e cuidadosamente controlada), quanto as tradicionais AdS/CFT é que ainda há dúvidas sobre isso que não temos satisfatoriamente respondido. As redes de tensores, por outro lado, estão extremamente concretas, objetos bem definidos, para os quais você deve, em princípio, ser capaz de responder a qualquer pergunta que possa ter. Talvez o mais intrigante, a ideia de “teoria das cordas” nunca realmente entrou no jogo. A “massa” onde a gravidade vive emerge diretamente de um conjunto de spins interagindo, num contexto em que os pesquisadores originais não estavam pensando sobre a gravidade em tudo. O ponto de partida nem sequer necessariamente tem algo a ver com o “espaço-tempo”, certamente não com a dinâmica da geometria do espaço-tempo. Então, eu certamente espero que as pessoas permaneçam animadas e continuem pensando nessa direção – seria revolucionário se você pudesse construir uma teoria completa da gravidade quântica diretamente de algumas interações.