No dia 06 de fevereiro de 2018, o mundo testemunhou um feito histórico: a empresa SpaceX lançou o Falcon Heavy, que é considerado o foguete mais poderoso em operação (só não é mais potente que o Saturn V, que levou o homem à Lua). Além disso, esse foguete carrega um Tesla Roadster como payload, que foi lançado ao espaço como parte de um teste para futuro envio de cápsulas tripuladas a Marte. Não contentes com isso, eles também testaram a volta dos três boosters ao solo com uma aterrissagem vertical espetacular. Uma pena que somente os boosters auxiliares conseguiram pousar com sucesso. Um teste parecido já havia sido feito pela empresa um tempo atrás, inclusive com aterrissagem em um navio plataforma, mas nunca em um lançamento com carga real.
Assistindo a um dos vídeos de retorno dos foguetes, me veio à mente que era possível fazer alguns cálculos simples pra determinar a distância aproximada entre câmera e os foguetes na hora em que eles ativaram os motores para o pouso e também a distância da câmera até a plataforma. É possível também calcular a que altura os foguetes estavam quando os motores reversos foram ativados. Tudo isso usando física de ensino médio. Nosso cenário fica parecido com o desenho abaixo:
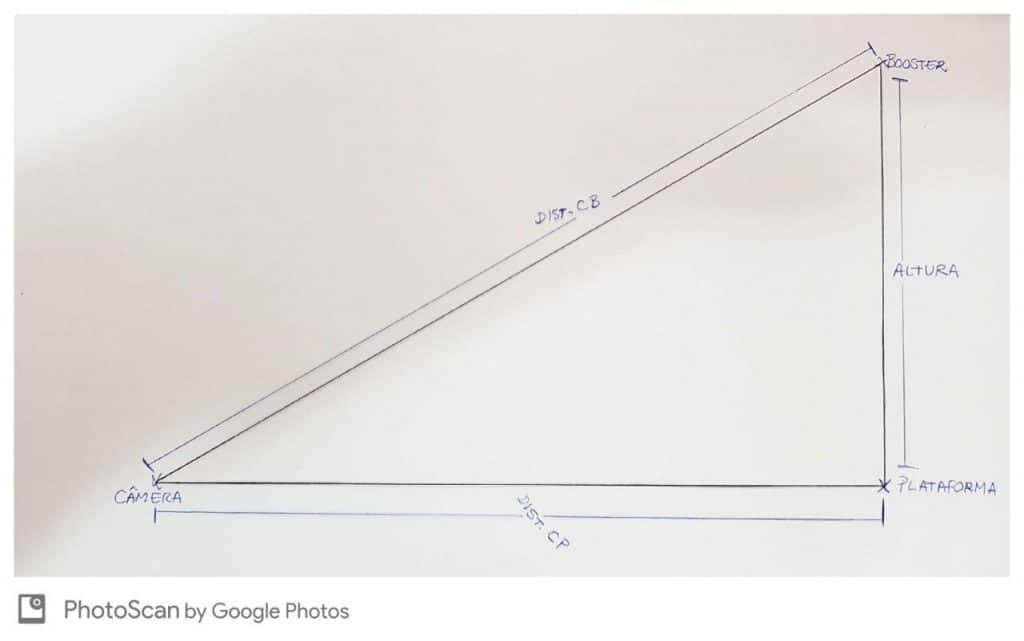
Isso é possível apenas assistindo a um vídeo por causa da enorme diferença de velocidade entre o som e a luz. Perceba que assim que os motores reversos são ativados, nós não ouvimos nada, mas depois de quase 10 segundos podemos escutar seis explosões estrondosas (sonic booms), agrupadas em dois grupos de três (cada grupo de explosões pertence a um dos boosters). A câmera ouve as explosões atrasada porque a velocidade do som é muito menor que a da luz, o que faz com que consigamos ver a explosão muito antes de o som chegar aos nossos ouvidos, ou ao microfone da câmera:
Vsom = 343m/s
Vluz = c = 299,792,458 m/s
Uma pequena observação sobre a velocidade da luz: aqui eu estou considerando o vácuo como meio. A velocidade da luz no ar (ou em qualquer outro meio) é a mesma, porém, os fótons são absorvidos pelos átomos e então re-emitidos, o que causa um atraso. Esse atraso faz com que eles demorem um pouco mais na viagem, causando a sensação, para um observador externo, de que a velocidade da luz é menor em meios que não o vácuo.
A partir daí, descobrir a distância entre os foguetes, no momento do início da queima final, e a câmera é fácil. Só precisamos contar quantos segundos se passam entre vermos o início da queima e ouvirmos a explosão. Já que o som viaja 343 metros a cada segundo, multiplicando 343 pelos segundos medidos nos dá essa distância.
Segundos entre visão e audição da explosão medidos: aproximadamente 8,85s
Distância CB = 8,85seg x 343m/s ~ 3035m
Sabemos agora que a câmera está a aproximadamente 3,035km de distância dos foguetes no momento em que eles ativam os motores reversos.
Agora precisamos fazer a mesma coisa para descobrir a distância entre a câmera e a plataforma, mas dessa vez precisamos contar o tempo entre vermos o pouso e pararmos de ouvir a queima dos motores (estou considerando o foguete mais próximo do solo nas contas). Só que isso nos deixa com um pequeno problema: a fumaça deixada nos pousos dificulta muito a visualização mais precisa do momento do pouso e desligamento dos motores. A ideia que tive foi tentar sincronizar esse vídeo com o vídeo que mostra o pouso visto da plataforma, assim podemos medir mais precisamente.
Após fazer a sincronização dos vídeos, o tempo medido entre avistarmos o pouso e pararmos de ouvir os motores foi de aproximadamente 6,20 segundos, o que nos dá:
Distância CP = 6,20seg x 343m/s ~ 2133m
Como alguns já podem ter notado, nosso esquema forma um triângulo retângulo, e nós temos os valores de dois de seus lados. Só nos resta agora descobrir a que altura os boosters estavam quando a queima final começou. Para isso, basta aplicarmos o famoso teorema de Pitágoras:
a² + b² = c²
Onde:
a = Distância CP
b = altura
c = Distância CB
Substituindo os valores:
2133² + altura² = 3035²
altura = √(3035² – 2133²)
altura ~ 2160m
Portanto, concluímos que a altura dos boosters até a plataforma é de aproximadamente 2160m, ou seja, maior que a distância entre a câmera e a plataforma, o que torna o nosso desenho anterior proporcionalmente incorreto. Porém, já sabíamos que isso poderia acontecer.
Essa matemática não foi feita com a precisão adequada, sei disso. Mas o propósito aqui foi mostrar que conseguimos estimar com uma aproximação bem razoável algumas informações bem bacanas sobre o evento, como, por exemplo, o fato de que os boosters auxiliares só começaram sua queima de aterrissagem há aproximadamente 2,16km de distância do solo. Pode parecer muito, mas não é.





