Por Robyn Arianrhod
Publicado na Cosmos Magazine
Um animado debate enfureceu a Europa do século XVIII sobre o que conduzia o movimento dos planetas. Na Inglaterra, Sir Isaac Newton e seus seguidores disseram que era a gravidade: a mesma força invisível que impulsiona uma maçã caindo também mantinha os planetas em seus caminhos maravilhosamente ordenados.
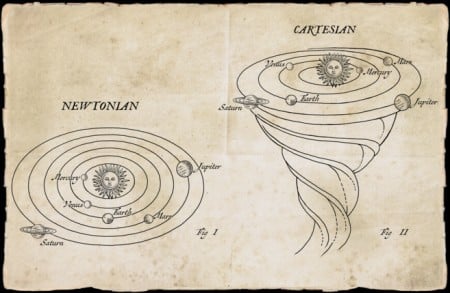
Do outro lado do Canal da Mancha. muitos Continentais preferiam a teoria de René Descartes que dizia que um “éter” cósmico giratório, como um tornado celestial, empurravam os planetas em seu caminho.
Esta discordância é mais do que uma curiosidade histórica – ela foi afundo do que é necessário para uma proposta se qualificar como uma verdadeira teoria científica.
Um par improvável ajudou Newton a conquistar a vitória na Europa Continental: o mais conhecido e mais polêmico dramaturgo da França, Voltaire, e sua amante, a matemática Émilie du Châtelet. Seu trabalho científico inclui o que ainda é a tradução definitiva em francês do Principia de Newton. No entanto, após sua morte, ela foi praticamente esquecida. Se ela foi lembrada, suas realizações foram muitas vezes menosprezadas, perdida na sombra dos “grandes homens” de sua vida. Mas os historiadores modernos têm redescoberto Émilie, e sua história está inspirando novas gerações de matemáticas mulheres, inclusive eu.
Quando Émilie mudou-se para Cirey para se juntar a seu amante, as más-línguas se alvoroçaram.
Nascida em Paris em 1706, ela é sem dúvida a matemática mais glamorosa da história. Alta e aristocrática, apaixonada por suas atividades intelectuais e amorosas, ela era maior que a vida. Muito ousada para a maioria das pessoas da época: ambiciosa demais, intelectual demais, emocional demais, e sexualmente liberal demais. Feminista demais também: ela não brincou enquanto escrevia sobre sua luta para graduar-se em matemática e física (as mulheres eram impedidas de entrar em boas escolas, ficando sozinhas nas universidades): “Se eu fosse rei” escreveu, “Eu reformaria esse abuso em cortar metade da humanidade. Eu teria mulheres participando de todos os direitos humanos, e, acima de tudo, os da mente”.
Aos 26 anos, ela cativou Voltaire, que foi seduzido por seu cérebro, bem como pela sua beleza. Ele já era famoso como um plebeu arrogante com um humor perverso. Émilie, ao contrário, nasceu para a vida aristocrática; seu pai tinha sido chefe de protocolo na corte de Luís XIV em Versalhes. Ela tinha sido casada aos 18 anos com o Marquês du Châtelet, com quem ela logo teve três filhos. Tendo feito o seu dever para a linhagem de Châtelet, ela e seu marido, em seguida, viveram vidas relativamente separadas – uma situação comum nas famílias aristocráticas. Menos comum era a amizade notável que eles desenvolveram, de modo que, finalmente, o marquês apoiou não só a ambição incomum de Émilie, mas também sua relação passional com Voltaire. Ter um amante era comum na época dos casamentos arranjados, mas Émilie e Voltaire escandalizaram a sociedade quando eles foram morar juntos: casos amorosos extraconjugais deveriam ser flertes discretos, não casamentos alternativos. Curiosamente, o arranjo interno dos dois – e seus papéis como revolucionários newtonianos – eram tão interligados quantos os mistérios do cosmos que eles queriam explicar.
A atração de Voltaire por Newton nasceu da raiva do dramaturgo pelos conservadores e pelas elites francesas – algo que ele deixou claro em sua escrita satírica. No momento em que ele conheceu Émilie em 1733, sua propensão em perturbar pessoas poderosas já tinha o levado à Bastilha por 11 meses – e no final da década de 1720 ele foi forçado a se exilar por alguns anos. Exílio esse que se mostrou feliz, pois ele tinha ido para a Inglaterra, onde conheceu alguns dos principais discípulos de Newton – o próprio Newton já passava de seus 80 anos nessa época..
Londres estava alvoroçada com Newton, e quando o grande homem morreu em 1727, Voltaire compareceu ao seu funeral na Abadia de Westminster. Tal veneração oficial de um cientista era desconhecida na França de Voltaire, e o deixou muito impressionado. Tanto que ele escreveu uma série de ensaios sobre os ingleses: sua monarquia constitucional, relativa tolerância religiosa, a ciência newtoniana racional, e a nova geração de filósofos empiristas, especialmente John Locke, amigo e discípulo de Newton.
Voltaire publicou esses ensaios na Inglaterra. No início de 1734, ele disse a um amigo que estava adiando a publicação da versão francesa mais longa – Lettres Philosophiques – por medo do clero da corte francesa. A edição francesa incluiu uma crítica desfavorável dos escritos religiosos do matemático francês Blaise Pascal, e uma defesa da afirmação de Locke de que o pensamento pode surgir através de um mecanismo material – uma ideia que deixou os teólogos nervosos de ambos os lados do Canal por assumirem que Locke estava dizendo que não existiam coisas como almas imortais.
A confusão com o dogma religioso era perigoso. Mas o apoio que Voltaire encontrou nas ideias de Locke e de Newton também desafiou o orgulho nacional francês. Um de seus ensaios criticou os “cartesianos” que dominavam a Academia de Ciências de Paris. Estes homens – seguidores do filósofo do século XVII René Descartes – tiveram grande dificuldade com a teoria do movimento planetário de Newton. Como a gravidade do Sol poderia viajar através de milhões de quilômetros no espaço vazio para alcançar e influenciar os planetas? Eles pensaram que isso cheirava a pseudociência – como a astrologia ou a alquimia. Isso é irônico, em retrospectiva, porque hoje nós consideramos a teoria de Descartes como pseudocientífica, com seus vórtices giratórios de éter invisível arrastando os planetas em suas órbitas. Ninguém sabia do que era feito esse éter, ou por que ele girava como um tornado. Voltaire apontou a hipocrisia de acreditar em redemoinhos etéreos mágicos enquanto rejeitavam a atração gravitacional. Seu ensaio mostra que para muitos teóricos do século XVII, as regras sobre o que constitui uma teoria verdadeiramente científica ainda não tinha solidificado.
A matemática foi crucial para a abordagem de Newton. Não que Voltaire estivesse no topo das sutilezas matemáticas que mostraram o quão superior a teoria de Newton era – ele precisaria da ajuda de Émilie para isso. Mas essa ajuda teria de esperar porque em abril de 1734, a editora francesa de Voltaire lançou o Lettres na França sem a sua permissão. Um mandado de prisão foi emitido e Voltaire passou a se esconder. Émilie se enfureceu com seus amigos pelo tratamento injusto que a França deu ao seu maior escritor. Seus apelos às autoridades, assim como os de seu marido e outros amigos aristocráticos, deu frutos. Voltaire foi autorizado a voltar para a França, onde viveu sob uma espécie de prisão domiciliar em no château de Cirey, em Champagne.
Quando Émilie se mudou para Cirey para se juntar a seu amante, as más-línguas se alvoroçaram, com ódio, porque ela tinha se atrevido a desrespeitar as regras do decoro. Ela e Voltaire começaram a transformar Cirey em uma academia informal onde estudavam, escreviam, discutiam filosofia e hospedavam intelectuais livres-pensadores. Era um arranjo idílico, embora às vezes Voltaire sentia que não estava trabalhando duro o suficiente em sua poesia e peças teatrais. “Muitas vezes”, disse ele, “a ceia, Newton e Émilie me levam embora”. Ele estava se referindo aos seus preparativos para uma popularização séria das ideias de Newton, que se chamaria Elementos da Filosofia de Newton.

Émilie levaria esse projeto ainda mais longe em um “comentário” de 180 páginas que ela anexou à sua tradução do Principia de Newton. Isto incluiu um guia do leitor relativamente acessível para os principais argumentos na teoria gravitacional do movimento planetário de Newton. Também descrevia as aplicações da teoria de Newton por seus eminentes amigos matemáticos e, por vezes tutores, Alexis Clairaut e o arrojado Pierre-Louis Moreau de Maupertuis, bem como uma atualização sobre a teoria da gravitação das marés de Newton por seu colega, o matemático suíço Daniel Bernoulli. O apêndice de Émilie também incluiu sua própria reformulação de algumas das provas mais importantes da linguagem do cálculo do Principia. Newton (e independentemente o matemático-filósofo alemão Gottfried Leibniz) inventou o cálculo – a matemática que descreve e prediz como as coisas mudam, como a posição de uma maçã que cai ou um planeta no céu. Mas, aparentemente, Newton sentiu que o cálculo era novo demais para convencer as pessoas da validade de sua radical teoria gravitacional . Em vez disso, ele estabeleceu a maior parte de seus argumentos com provas geométricas engenhosas mas idiossincráticas – o tipo de abordagem lógica, rigorosamente aperfeiçoada pelos gregos antigos. Émilie re-escreveu algumas dessas provas usando a notação dy/dx que havia sido desenvolvida por Leibniz.
A fama de Émilie entre os intelectuais europeus não veio de sua tradução do Principia, mas a partir de um trabalho anterior de ciência popular – chamado Institutions de Physique (Fundamentos de Física) – no qual ela corajosamente tentou integrar o trabalho de Newton e Leibniz. A opinião científica naquele tempo tenderam a favorecer tanto o inglês quanto o alemão. Não foi apenas sobre nacionalismo, foi também um debate sobre o que constitui uma teoria da natureza. Newton focou em fornecer explicações testáveis para o que podemos observar no Universo, enquanto Leibniz enfatizou questões filosóficas sobre a natureza da existência. O brilhantismo de Émilie estava em sua capacidade de compreender as sutilezas da teoria de Newton e filosofia de Leibniz.
Voltaire, por outro lado, estava extasiado com Newton e não se preocupou muito com Leibniz – ele e Émilie permaneceram em desacordo sobre a questão. Em sua novela, Candide, ele iria satirizar a filosofia de Leibniz sobre o “melhor mundo possível” – tentativa de Leibniz de conciliar a bondade de Deus com o sofrimento e o mal no mundo.
Em meados da década de 1740, no entanto, o trabalho de Emilie no Principia estava mais próximo a seu coração – traduzir 500 páginas de Latim e geometria complexa, e verificar e re-verificar suas provas de cálculo, foi árduo. “Eu nunca fiz esse sacrifício para a razão, por isso eu tenho que ficar aqui e terminar este livro. É um trabalho horrível, para o qual é necessário uma cabeça e uma constituição de ferro”, ela lamentou. No entanto, tanto ela como Voltaire estavam seduzidos pela lógica de Newton. Mostrando quão profundamente a mente humana pode penetrar os mistérios da natureza, Newton deu aos seus discípulos esperança de que a razão iria triunfar sobre a superstição, dando início a uma abordagem racional, secular, não só para a “filosofia natural”, mas também para a política e para a ética.

Em particular, Émilie e Voltaire perceberam que Newton tinha criado o modelo para a física teórica moderna. Ele fez isso para manter a religião e a filosofia separadas do que podemos realmente observar, e pelo que podemos inferir a partir dessas observações. Os cartesianos, por outro lado, pertenciam ao passado – uma era em que os teóricos científicos eram principalmente filósofos. A tarefa do filósofo natural não era tanto medir e quantificar, e sim ser metafísico – olhar “além” das observações físicas para encontrar a causa final ou a natureza de um fenômeno. Pense na hipótese do éter giratório: era uma tentativa de imaginar o que poderia estar causando o movimento dos planetas, e era consistente com a noção de “auto-evidência”, onde as forças devem fazer contato direto com os objetos para movê-los. Mas não havia nenhuma evidência para esta substância etérea. A teoria do éter não faz nenhuma previsão sobre os movimentos reais dos planetas. Na verdade, Newton mostrou que um vórtice matemático era incompatível com as observações planetárias do astrônomo alemão Johannes Kepler.
Newton, por outro lado, começou com as análises de Kepler (Kepler, por sua vez, passou anos peneirando as observações do astrônomo dinamarquês Tycho Brahe sobre as posições dos planetas no céu em diferentes épocas do ano). Kepler foi capaz de ajustar uma curva matemática para a órbita de cada planeta e percebeu que eles formavam elipses em torno do Sol. Ele também encontrou relações entre o tamanho de uma órbita e o tempo que o planeta leva para orbitar o Sol. As leis de Kepler forneceram uma descrição matemática precisa dessas órbitas.
Mas o objetivo de Newton era desenvolver uma teoria sobre o por quê dos planetas se moverem.
Newton utilizou a análise de Kepler para mostrar que a força necessária para mover um planeta em uma órbita elíptica em torno do Sol deve obedecer a uma “lei do inverso do quadrado”. Isto é, como a distância a partir do sol aumenta, a força torna-se mais fraca; por exemplo, se a distância aumenta duas vezes, a força é apenas um quarto do que era antes – o inverso do quadrado de dois. Então planetas mais longe do Sol experimentam menos força e têm órbitas mais amplas, mais lentas. Newton também mostrou que luas com órbitas circulares, e cometas cujas órbitas eram elípticas, parabólicas ou hiperbólicas, também eram regidas pela mesma lei.
Mas a genialidade de Newton não parou por aí: ele percebeu que essa força do inverso do quadrado celestial era a mesma força que faz com que as maçãs caiam na Terra. Em outras palavras, planetas e luas estavam caindo em torno de seu “hospedeiro”. Galileu tinha explorado a natureza da aceleração devida à gravidade rolando bolas de metal em uma prancha, publicando seus resultados em 1638, 49 anos antes da publicação do Principia. Para mostrar que essa mesma força gravitacional estava agindo na Lua, Newton calculou a aceleração circular da Lua (com base na sua velocidade e distância da Terra) e descobriu que ela tinha cerca de 1/3600 da aceleração de um corpo em queda aqui na Terra. A Lua está cerca de 60 vezes mais longe do centro da Terra do que nós na sua superfície, de modo que a lei do inverso do quadrado funcionava!
Claro, a linha de raciocínio de Newton era muito mais complexa do que isso. O que é importante, a partir de uma perspectiva moderna, é que a sua teoria poderia ser utilizada para fazer previsões testáveis. Newton viveu para testemunhar uma de suas primeiras confirmações – o eclipse solar total de 1715 que causou a escuridão em toda a Inglaterra, norte da Europa e norte da Ásia. Foi uma ocasião pública emocionante, mas uma confirmação ainda mais espetacular veio 32 anos depois de sua morte: o retorno do cometa Halley em 1759.
Na década de 1730 e 40 Émilie e Voltaire ajudaram a articular e popularizar a extraordinária conquista de Newton – uma mudança de paradigma em nossa compreensão do Universo. Em Elementos da Filosofia de Newton, Voltaire disse que a ênfase cartesiana sobre as causas metafísicas era “a maneira mais segura de perder o nosso caminho. Em vez disso, [como Newton] vamos seguir passo a passo o que realmente acontece na natureza: como exploradores que chegam na foz de um rio, é preciso viajar até o rio antes imaginando onde sua fonte está localizada”.
Nem mesmo os grandes contemporâneos de Newton Leibniz e Christiaan Huygens haviam entendido o paradigma de Newton: eles concordavam que a teoria da gravidade era um tour de force que combinava notavelmente bem com as evidências físicas da movimento planetário. Mas eles não estavam convencidos que a gravidade poderia atual em toda a vastidão do universo. Uma vez que Newton não tinha dado nenhuma ideia de como isso poderia acontecer, eles rejeitaram sua teoria como um retorno ao misticismo.
Newton tinha, de fato, tentado sem sucesso encontrar um mecanismo pelo qual a gravidade funcionasse, mas ele se recusou a incluir especulações não testadas em seu rigoroso Principia. Ele deixou tal descoberta para a posteridade (de Einstein, até agora), dizendo: “É o suficiente que a gravidade realmente exista e aja de acordo com as leis que temos estabelecido, e isso é o suficiente para explicar todos os movimentos dos corpos celestes e do nosso mar [as marés]”. O suficiente de fato: hoje sabemos que, para a maioria das aplicações no âmbito do Sistema Solar, a teoria de Newton tem uma precisão de uma parte em dez milhões.
Mas nem mesmo Newton tinha todas as respostas – especialmente quando se tratava da natureza da luz e do calor. Em 1738, esta era uma questão tão em aberto que a Academia de Ciências de Paris a tornou tema de seu concurso de redação anual, que Voltaire planejou entrar. Ele e Émilie tiveram um laboratório impressionante com um grande telescópio refletor, prismas de alta qualidade, lentes e escalas de medição precisos. Eles ficaram fascinados com experimentos de ótica de Newton – incluindo aqueles que provaram que a luz branca é composta pelo espectro de cores. Mas Newton não tinha uma teoria sobre a composição fundamental da luz, embora ele tenha sugerido que era feita de minúsculas partículas.
Voltaire assumiu que o calor também era feito de partículas. Com a ajuda de Émilie ele aquecia enormes quantidades de metal na fornalha de Cirey, pesando o metal antes e após o aquecimento para ver se ele poderia detectar um aumento na massa – a massa das partículas de calor adicionais. Depois de meses ele não tinha resultados consistentes, e Émilie começou a acreditar o calor não tinha peso. Voltaire era tão apaixonadamente newtoniano que não quis ouvir seus argumentos – que incluíam a possibilidade de que o carvão vegetal estranhamente revestia o metal, de modo que a experiência nunca poderia funcionar.
Émilie também acreditava, ao contrário de Newton, que a luz não tinha peso. Sua conclusão foi baseada em uma experiência de pensamento engenhoso. Ela calculou que, mesmo que uma partícula de luz pesasse menos de um trilionésimo do peso de uma bala de canhão, a sentiríamos como uma bala de canhão quando atingisse os nossos olhos por causa da sua velocidade!
Ela tinha outras ideias inovadoras sobre a luz e o calor, também – por exemplo, que as diferentes cores da luz teriam quantidades diferentes de energia e temperaturas diferentes, uma conjectura que seria confirmada meio século mais tarde. Émilie não testava as suas ideias sobre a luz e o calor com experimentos. Mas ela os expressou em uma entrada individual para o concurso de redação da Academia de Paris. Ela entrou anonimamente e em segredo. Ela não queria ferir os sentimentos de Voltaire por discordar publicamente com ele – e não queria expor-se ao ridículo, como uma mulher que se atreveu a entrar no território masculino. A única pessoa que ela confiava seu segredo era seu marido! (Ele se juntou a família Cirey durante pausas raras de seu serviço militar – e de suas amantes.)
Como se viu, Voltaire ficou orgulhoso do ensaio de Émilie, e pensou que ela deveria ter ganho a competição. E ela pensou que ele deveria ter ganho: ela reclamou a um amigo que os acadêmicos eram muito cartesianos para serem imparciais. Mas não eram tão parciais a ponto de não concordarem que cada um dos artigos de Cirey eram suficientemente interessantes para publicação, juntamente com os vencedores, nos processos da Academia. E assim Émilie tornou-se a primeira mulher a ter um artigo científico publicado nesta revista de prestígio.

Émilie esperava seu trabalho sobre Newton vivesse para sempre. Mas logo depois de sua morte, sua reputação científica desapareceu também. Voltaire perdeu o interesse na ciência, e seu Principia definhou em uma gaveta – até Clairaut o imprimir pela primeira vez. Ele checou suas provas de cálculo nos meses antes de morrer, e ele tinha refinado os cálculos de Newton e de Halley para obter a previsão precisa do retorno do cometa Halley em 1759. Que melhor celebração do que publicar o livro de Émilie no mesmo ano! Ela teria ficado encantada: ela sabia que o cometa era uma chave para assegurar a reputação de Newton.
E estou muito contente por poder comemorar suas realizações aqui, e para honrar o sacrifício que ela fez “para a razão”. Ela foi uma inspiração para mim na minha própria jornada na matemática de nível superior, e ela continua a inspirar as mulheres – e homens – por causa de suas realizações matemáticas contra quaisquer probabilidades, e sua coragem em viver a vida ao máximo.
O que torna uma teoria grande hoje?

A tecnologia abriu uma janela para um universo que parece mais misterioso do que há três séculos atrás. Estamos deslumbrados pela energia escura, matéria escura, multiversos que consistem não apenas no nosso próprio “melhor mundo possível” – mas todo mundo possível. O que aconteceu com o método de Newton: partir de um conjunto de princípios físicos e leis matemáticas para chegar em uma bela teoria? Algumas dessas novas ideias parecem nos levar de volta ao éter de Descartes.
Mas Newton provavelmente teria tido dificuldades com as nossas estranhas teorias modernas. Assim como sua teoria da gravidade, as teorias modernas dão saltos ousados que os cartesianos jamais aceitariam. Nós ainda não sabemos realmente o que a gravidade é, então o que os cartesianos fariam com tais ideias contra-intuitivas como a equivalência massa-energia, ou o espaço-tempo curvo ou a antimatéria? Embora essas ideias sejam estranhas, elas surgiram a partir de teorias baseadas, como a de Newton, em experiências e matemática – ao contrário do éter.
Uma grande teoria não precisa ser – na verdade, não pode ser – um ajuste perfeito para o mundo físico. A teoria da gravitação de Newton foi há muito tempo incorporada na teoria da relatividade geral de Einstein, que, sem dúvida, precisa de atualização à medida que aprendemos mais sobre o Universo. No entanto, ambas as teorias previram com sucesso uma física nova e inesperada, e eles permanecem extremamente precisos: a teoria de Newton se encaixa na observação do movimento planetário melhor do que 0,0001%, enquanto a teoria de Einstein passou em todos os testes experimentais até agora. É por isso que eles sempre serão o que Roger Penrose chamou, em Nova Mente do Imperador, de teorias “magníficas”. (Outras nesta categoria incluem a teoria de Maxwell sobre o eletromagnetismo, a eletrodinâmica quântica e a mecânica quântica.)
Durante o processo de encontrar novas teorias, ou adaptar as antigas para que elas se ajustem a dados mais precisos, todos os tipos de conjecturas selvagens emergem e debates acalorados surgem. Usando a terminologia de Penrose, essas teorias emergentes podem ser categorizados como “úteis” – como o modelo padrão do Big Bang – ou “tentativas” – como o modelo cíclico do universo, ou a teoria das cordas que une a gravidade com as outras forças fundamentais. A teoria será “magnífica” somente quando ela fizer previsões que forem experimentalmente confirmadas em um alto nível de precisão e com uma vasta gama de aplicações ou explicações.





