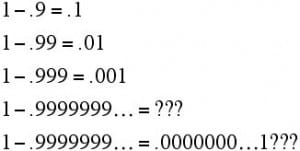Possivelmente, um dos temas mais polêmicos da matemática atualmente são as infames provas de que $latex 0.999… = 1$
A mais clássica e comum delas é a prova usando fração geradora:
Proposição: $latex 0.999… = 1$
Prova: Tome $latex x = 0.999…$
Multiplicando por 10 dos dois lados:
$latex 10x = 9.99….$
Subtraia então x dos dois lados:
$latex 10x-x = 9x = 9.999… -x = 9.999… – 0.999 = 9$
E de 9x = 9 segue x=1.
Além dessa tem outra bastante comum que parte de 1/3 = 0.333…, então multiplique por 3 dos dois lados e resta 3/3 = 1 = 0.999… . Essas duas provas são frequentemente contestadas, alguns afirmam que resta 0.000….1 de diferença entre 1 e 0.999…, essa uma casa decimal após infinitos zeros. Outros afirmam que 1 = 0.999… é uma colocação errada, e que o correto seria dizer que 0.999… TENDE a 1.
Apesar de tanta polêmica, uma questão que nunca é atacada – e que está no cerne do problema – é o que SIGNIFICA 0.99999…? Ou melhor, o que significa no geral essas representações decimais infinitas?
Então, tomemos a mentalidade dos matemáticos, vamos resolver um problema: Dar significado a expansão decimal infinita! Para isso vamos assumir que entendemos bem a representação usando frações, e vamos assumir também que sabemos dos números reais (e paramos neles, não entraremos em Complexos, Hiper-reais ou Surreais).
É razoável antes de partirmos para números com INFINITAS casas decimais, motivar o que queremos usando números que conhecemos bem, e nos guiar com isso. Tomemos um número comum: 1/2, o ponto intermediário entre os números 0 e 1, queremos uma forma de representar ele sem precisar recorrer a ideia de divisão, então, vamos pensar nos números como uma reta, dividindo o caminho entre 0 e 1 em 10 intervalos iguais, e numerando eles, tomamos o meio do caminho, que é 0 5:

Motivado por isso, dividimos o caminho entre 0 e 1 em 10 partes e tomamos a quinta delas, ou seja, estamos 5/10 do caminho, o que faz sentido, pois queremos manter, 5/10 = 1/2. Então, vamos representar o 5/10 de outra forma, vamos definir:
$latex \frac{5}{10} = 0.5$
E nossa notação decimal para uma casa se mostra uma forma rápida de representar uma divisão por 10. De forma análoga podemos reduzir nossa escala em 10 e achar o meio do caminho entre 0.5 e 0.6 como sendo 0.5 + 5/100, e chamar isso de 0.55, o que é consistente com o que queremos. Baseado nisso podemos então definir de forma consistente a representação decimal finita.
Definição (provisória): Sejam $latex a_1, a_2, …, a_n$
Dígitos entre 0 e 9, então dizemos que:
$latex 0.a_1a_2a_3…a_n = \frac{a_1}{10} +\frac{a_2}{10^2} +\frac{a_3}{10^3} + … + \frac{a_n}{10^n} = \Sigma_{i = 1}^n \frac{a_i}{10^i}$
Agora temos uma definição consistente com 0. 5 = 5/10 = 1/2 como queríamos. Podemos com ela encontrar a expansão decimal de várias fracões, escrevendo elas em termos de somas frações divididas por expoentes de 10, por exemplo:
$latex \frac{492}{4000} = \frac{400+80+12}{4000} = \frac{1}{10} + \frac{2}{100} + \frac{3}{1000} = 0.123$
Mas nossa definição está longe de perfeita, pois vamos cair num problema com expansões decimais da forma 1/3:
$latex \frac{1}{3}=(\frac{9+1}{3})\cdot \frac{1}{10} =\frac{3}{10} + (\frac{1}{3}) \frac{1}{10} = \frac{3}{10} + \frac{3}{100} + \frac{1}{300} = …$
Não importa o quanto tentarmos isolar um número finito de termos, sempre acaba existindo algum termo que não está na forma que queremos para escrever a expansão decimal, temos algo da forma 1/3 = 3/10 + 3/100 + 3/1000…!
E assim até o infinito! Então, temos que modificar nossa definição de forma a permitir infinitos dígitos após a virgula, mas será que podemos somar infinitos termos? Bem, a ideia de somar infinitos termos é conhecida na matemática como: Série, e para uma série ter uma valor bem definido ela precisa ser somável. Para o bem da linha de raciocínio, vamos assumir que todas as séries que podem aparecer devido a expansão decimal tem valores bem definidos (ou convergem) – Esse resultados sobre séries podem ser encontrados facilmente em livros de Cálculo.
Vou apenas introduzir um conceito curto que vai ser útil na definição geral, de forma não muito formal: uma sequência é um conjunto de números enumeráveis e ordenados. Ou seja, é uma sequência da forma: 1,3,5,1,6,8,1, 3.2, 1/2… onde sabemos cada elemento tem um lugar bem definido na ordem. Costumamos denotar o n-ésimo termo da sequência como:
$latex a_n = elemento_{aqui}$
E denotamos toda uma sequência por:
$latex \{a_k\}_{k \in \mathbb{N}}$
Agora podemos finalmente dar uma definição final e concreta para expansão decima: Seja
$latex \{a_k\}_{k \in \mathbb{N}}$
Sequência de dígitos de 0,…,9, então, definimos:
$latex 0.a_1a_2…a_n… = \Sigma_{k=1}^{\infty} \frac{a_k}{10^k}$
Ou seja, a expansão decimal é uma forma simplificada de denotar uma série, uma soma. E caso o tanto de casas decimais seja finito, basta adicionar zeros no resto final da sequência, ou seja, a definição é coerente com o que tínhamos antes. Estamos muito próximos de poder computar de fato a expansão decimal 0.999…, antes precisamos somente de um último resultado:
Seja r número entre 0<r<1, assuma então a série de suas potências converge (conhecido também como série geométrica): $latex \Sigma_{1}^{\infty} r^k = ?$
Caso a soma fosse finita, poderíamos usar os resultados de progressão geométrica para encontrar o valor, então vamos primeiro avaliar uma soma finita:
$latex \Sigma_{0}^{N} r^k = \frac{1-r^{N+1}}{1-r} = \frac{1}{1-r} – \frac{r^{N+1}}{1-r}$
Agora suponha que vamos tomar N cada vez maior – isto é, fazer N tender ao infinito, o segundo termo se vai a zero nesse limite, então a série converge, então, quando a série converge dizemos que ela é IGUAL a 1/(1-r):
$latex \Sigma_{k=0}^{\infty} r^k= \frac{1}{1-r}$
Dizemos que esses valores são iguais, assim como 1+1=2 e não 1+1 tende a 2. Agora vamos por fim computar a polêmica expansão decimal: 0.999…, que pode ser representada pela série acima:
$latex 0.999… = \Sigma_{k=1}^{\infty} (\frac{9}{10^k})= \frac{9}{10} \cdot \Sigma_{k=0}^{\infty} (\frac{1}{10^k}) = \frac{9}{10} \cdot \frac{1}{1 – \frac{1}{10}} = \frac{9}{10} \cdot \frac{10}{9} = \frac{9}{9} = 1$
E, dado a nossa definição de expansão decimal, vale que 0.999… = 1. Apesar disso, a ideia de existir um número infinitamente perto de 1 que não é 1, algo similar ao 0.000…1, não é uma ideia ruim! Ela da motivação a outras áreas da matemática, e a criação de coisas bastante estranhas, mas no contexto de números reais, não existe diferença entre 0.999… e 1, eles são o mesmo número, assim como 5 = 1 + 4, ou 20 = 20/1 = 40/2, são apenas diferentes maneiras de escrever o MESMO número!