“As 7 pontes de Konigsberg” é um problema que foi resolvido por Leonhard Euler em 1735. Sim, aquele preguiçoso que publicou cerca de 800 trabalhos…
O problema consiste no seguinte:
Na cidade de Konigsberg, Alemanha, um rio passava pela cidade e a dividia em quatro partes. Para interligar estas partes, havia sete pontes (daí o nome do problema). Dada a situação ilustrada na imagem, é possível (passando só uma vez por cada ponte) fazer um caminho que passe por todas elas?
Faça um esboço do mapa e tente traçar um caminho para responder que sim, ou seja, que é possível. Depois volte para terminar de ler o artigo.
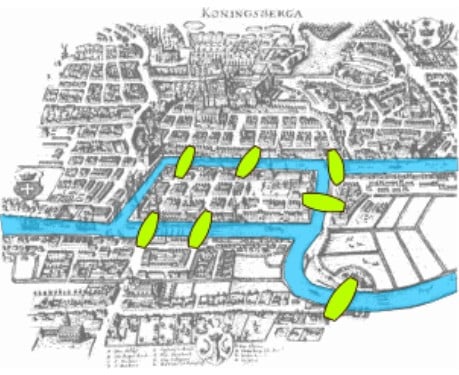
E aí, conseguiu? Não?! Mas isso é trivial… brincadeira. Euler também não conseguiu! É impossível traçar um caminho que passe só uma vez por cada ponte e, no final, tenha atravessado todas elas – Euler mostrou isso, elegantemente. No entanto, se o número de pontes fosse, digamos, seis, haveria tal caminho.

Para mostrar que era impossível responder que sim ao problema, Euler fundou uma área da Matemática que se chama Teoria dos Grafos, que é um modelo cujas preocupações estão nas relações entre pares de entidades. Ver a Teoria dos Grafos mais a fundo fica para a próxima. Por hora, vamos ter uma intuição de como ele respondeu a questão.
Primeiro, dá pra simplificar a imagem, já que não importa cor, formato e tamanho. A única coisa que precisamos é diferenciar pontes de não pontes.
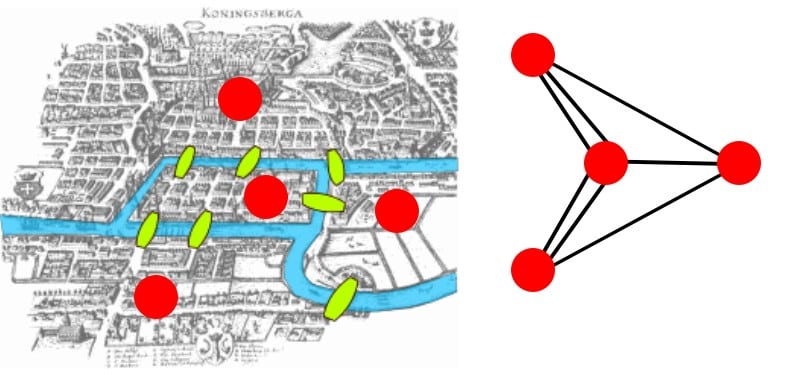
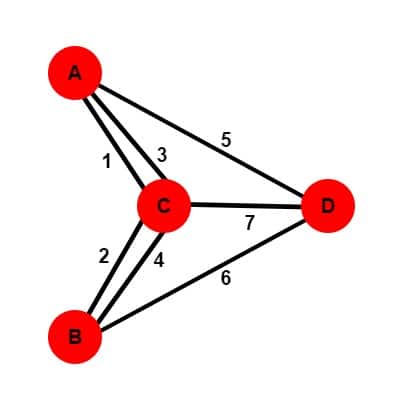
Vamos chamar as pontes de arestas e o que não são pontes de vértices, dessa forma o problema se torna mais genérico. Diremos também que o grau de um vértice é a quantidade de arestas que se conectam a ele.
Todo vértice vai ter um rótulo único que o representa, o mesmo vale para arestas, conforme a imagem que segue.
Neste grafo, cada vértice tem grau ÍMPAR. Os vértices A, B e D têm a mesma quantidade de arestas, três. C tem cinco.
Se você parte de um vértice com um número ímpar de arestas, você estará condenado a não terminar nele, caso queira percorrer todas as arestas só uma vez.
Pense comigo (mas por você): tenho três arestas. Saio por uma, restam duas. Volto por outra, sobra uma. Saio pela última. Não consigo mais voltar a este vértice, respeitando as condições impostas.
Se começo fora de um vértice V, e V tem número ímpar de arestas, o que acontece? Basta usar o mesmo raciocínio.
Com essa bagagem, podemos concluir que um vértice com grau ímpar deve ser onde começa ou termina nosso caminho!
Para o caso das pontes de Konigsberg, há quatro vértices de grau ímpar. Mas já vimos que tais vértices devem estar no início ou no fim (e só há um início e um fim), portanto, podemos ter no máximo dois vértices de grau ímpar para resolver o problema. Acho que concordamos que 4 > 2. Assim, é impossível traçar tal caminho, nas condições dadas.
Grafo é uma área muito extensa, isso que você leu é apenas a ponta do iceberg (se gostou, não pare por aqui). Apesar da teoria dos grafos pertencer à matemática, ela é muito importante na computação (talvez até mais nela). Com muito esforço, fazemos na mão um grafo com algumas dezenas de vértices e arestas. Mas e se a modelagem requer milhares, milhões ou até bilhões de vértices e/ou arestas? Aí entra a computação.
Algumas aplicações de grafos:
Redes de Transporte: Podemos modelar uma rede de transporte com grafo. Vamos supor que estamos interessados na conectividade entre um grupo de cidades. Os vértices podem ser as cidades (ex: São Paulo, Campinas, Ribeirão Preto, etc). Já as arestas, podem ser simplesmente a conexão direta entre duas cidades. Você ainda poderia dizer que as arestas guardam as distâncias duma cidade até outra (aí já entra o conceito de grafo ponderado, isto é, com peso nos vértices e/ou arestas).
Repare que usei “podemos”, “podem”, “poderia”, para dizer o que são os vértices e arestas deste grafo. Isso porque um sistema pode ser modelado de muitas maneiras, algumas pouquíssimo intuitivas. Tudo depende do problema que você quer resolver e da sua criatividade para modelar a questão.
Atores: Agora um exemplo menos útil, mas que serve pra mostrar o quão genérica é a teoria dos grafos. Quero ver, através dum grafo, alguns filmes em que determinados atores participaram juntos.
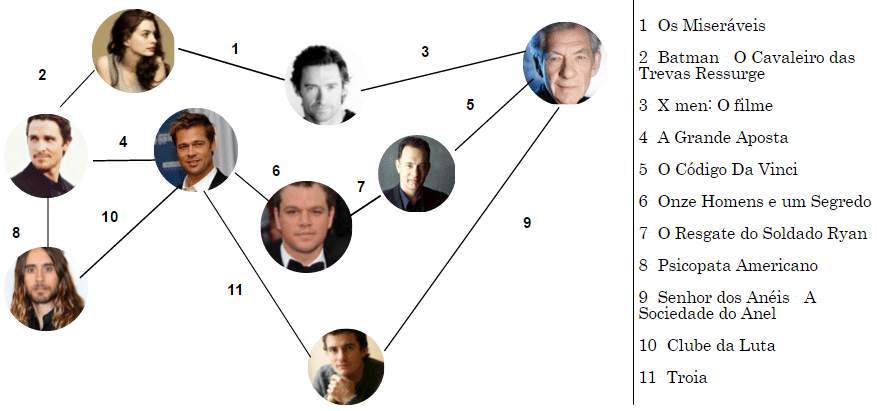
Nota: antes que os cinéfilos me enforquem, esse grafo não foi feito pra dizer todos os filmes onde determinado par de atores esteve.
Caso tenha alguma aresta indevida neste grafo, por favor, me avise.
Nos comentários, me diga algumas situações que você poderia modelar com grafos, definindo o que seriam vértices e arestas. É uma prática bem legal, a meu ver. Como não pensamos todos da mesma forma, acabamos aumentando nossa “inteligência” com as sacadas dos outros. Então, me ajude a ficar mais “inteligente”!
REFERÊNCIAS BIBLIOGRÁFICAS
- O Romance das Equações Algébricas – Gilberto G. Garbi – Livraria da Física – Quarta edição, 2010.
- Teoria de Grafos e suas Aplicações – Polyanna Possani da Costa – Dissertação de Mestrado – UNESP.
REFERÊNCIAS
- Graph Theory: 01. Seven Bridges of Konigsberg – <https://www.youtube.com/watch?v=eIb1cz06UwI&index=1&list=PLGxuz-nmYlQOiIOriTXMEoGoybUC3Jmrn> – Sarada Herke – Acesso em Março de 2016.
- Konigsberg Bridge Problem – <https://www.youtube.com/watch?v=2iovbcPwAro> – Acesso em Março de 2016.
- The Seven Bridges of Konigsberg – <https://www.youtube.com/watch?v=_OiZrmnni9Y> – Acesso em Março de 2016.
- (02-Caminhos Eulerianos) O problema das sete pontes – <https://www.youtube.com/watch?v=TmMyl16FByk> – Acesso em Março de 2016.
- Problema das pontes de Konigsberg – <http://www.inf.ufsc.br/grafos/problema/pontes/grafos.html> – Acesso em Março de 2016.
- As pontes de Konigsberg – <http://www.mat.uc.pt/~alma/escolas/pontes/> – Adérito Araújo – Acesso em Março de 2016.
- Euler e as pontes de Konigsberg – <http://www.seara.ufc.br/especiais/matematica/eulergauss/eulergauss4.htm> – Acesso em Março de 2016.
- Entenda o enigma das pontes de Konigsberg que instigou a geometria – <http://redeglobo.globo.com/globociencia/noticia/2011/12/entenda-o-enigma-das-pontes-de-konigsberg-que-instigou-geometria.html> – Acesso em Março de 2016.
- Grafos – <http://www2.ic.uff.br/~julius/icc/grafos.pdf> – Acesso em Março de 2016.