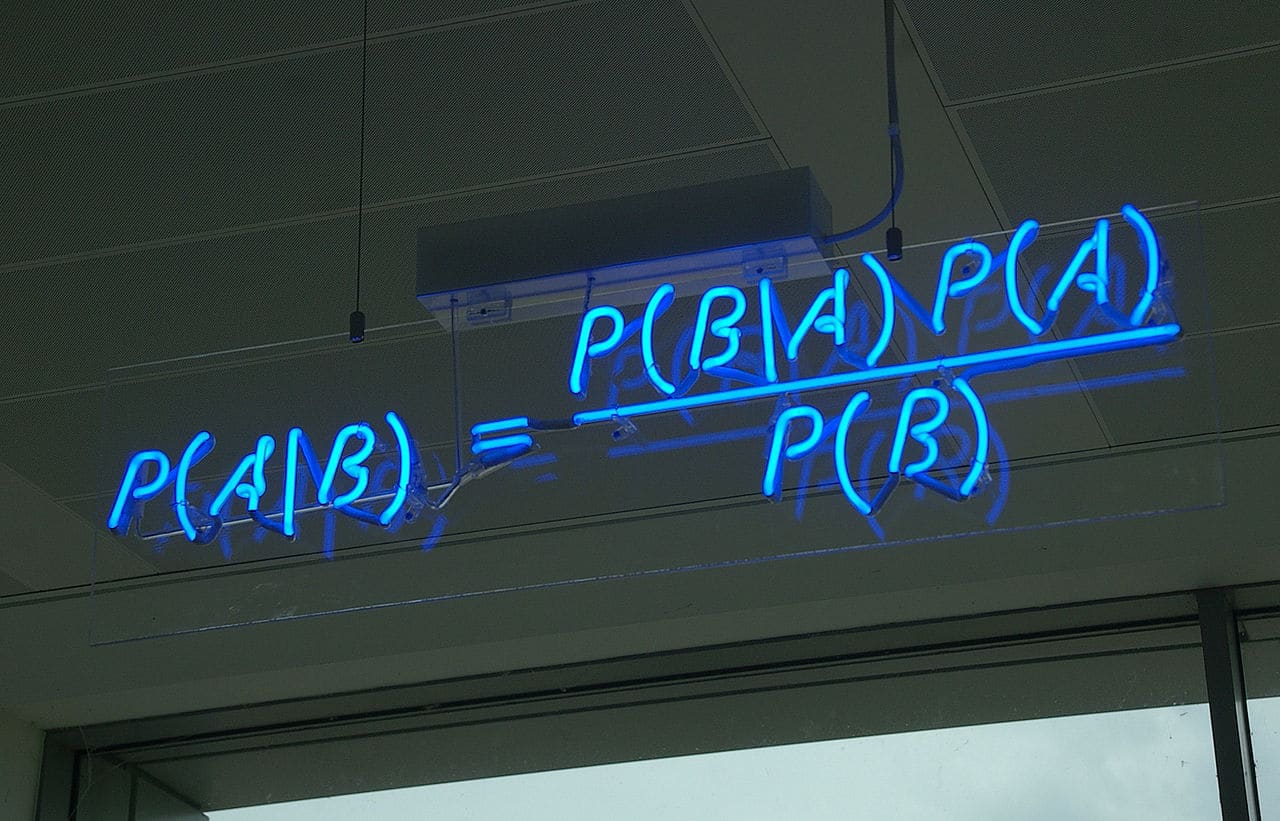Probabilidades subjetivas: admissíveis na ciência?

Por Mario Bunge
Publicado no Evaluating Philosophies

Bayesianismo é o alvitre de que probabilidades são questão de opinião. Isto é porque elas apenas mediriam a força de nossas crenças (De Finetti 1972; Jeffreys 1975; Keynes 1957; Savage 1954). Essa visão é geralmente conhecida como Bayesianismo por causa de sua forte dependência de uma certa interpretação do teorema de Bayes, uma peça de matemática pura que na verdade não se refere nem ao sujeito conhecido, nem ao mundo real.

Mais precisamente, de acordo com os Bayesianos, todas as proposições (ou declarações) qualificam-se como mais ou menos prováveis – embora não se preocupem em explicar o que se entende por “esta proposição é provável”, ou por “esta proposição é mais provável do que aquela”.

Bayesianos admitem que sua avaliação da probabilidade de uma determinada proposição é suscetível de diferir da minha. Mas, porque a probabilidade, como a beleza, estaria no olho do espectador, não há maneira de saber qual de nós está certo. De fato, como diz o estatístico que iniciou a fase contemporânea desta corrente, os bayesianos “sustentam que uma probabilidade, por ser apenas uma medida da crença de alguém, não é suscetível de ser provada ou refutada pelos fatos” (De Finetti 1962: 360). Qualquer coisa serve!

Meu objetivo neste capítulo é examinar o Bayesianismo para descobrir se ele é científico e, portanto, merece a atenção de cientistas, engenheiros, especialistas legais, médicos e outros especialistas. Para desempenhar essa tarefa, eu me inspirarei muito em alguns trabalhos anteriores (Bunge 1951, 1955, 1976, 1981, 1988, 2006, 2008, 2010).

1. Cuidado com a linguagem informal

O bayesianismo é popular fora da ciência e da tecnologia, em grande parte devido à confusão da palavra “probabilidade” em seu sentido matemático com seu homólogo de linguagem informal, que abrange conceitos tão diferentes como os de possibilidade, frequência, plausibilidade e verossimilhança.

Há mais de dois séculos, o bayesianismo penetrou a lei, onde às vezes é chamado sarcasticamente como “julgamento por números”. Assim, de acordo com um jurado em quase qualquer julgamento, o réu é “provavelmente” inocente, enquanto outro jurado jura que o mesmo indivíduo é “provavelmente” culpado. Além disso, enquanto um juiz pode afirmar com segurança que um determinado criminoso é “provavelmente” um reincidente, ele pode decidir que outro indivíduo “provavelmente” desistirá de uma carreira no crime. Não surpreendentemente, no Texas, a lei exige que os jurados considerem “se há uma probabilidade de que o réu cometa atos criminosos de violência que constituam uma ameaça para a sociedade”. Lamentavelmente, os jurados não são instruídos sobre como avaliar tal “probabilidade “: Presumivelmente, eles são esperados a usar o bom senso para decidir sobre a vida de uma pessoa.

O que fazer diante de tais incertezas? Um cientista presumivelmente recomendaria revisar todas as evidências do caso, convocar mais especialistas, ou talvez verificar as circunstâncias de alguns jurados para se certificar de que eles não foram nem subornados nem intimidados. Não é assim um jurista erudito da persuasão bayesiana: Ele plausivelmente (não “provavelmente”!) sugeriria que se aplique o famoso teorema do Júri de Condorcet: Aumentar o número de jurados, independentemente de suas qualificações e da qualidade das evidências existentes.

Mas é claro que é implausível ao jurista comprado no Bayesianismo exibir qualquer evidência empírica para ou contra a verdade do dito teorema, se apenas porque o próprio conceito de verdade não ocorre no Bayesianismo, que é radicalmente subjetivista, e, portanto, relativista. Então “nosso sábio amigo” pratica a lei baseada em evidencia nenhuma de qualquer forma. O nariz substitui o córtex frontal, consequentemente o tribunal irregular substitui a legítima corte da lei.

A ausência conspícua dos conceitos de verdade objetiva e evidência deve ser suficiente para alertar o jurista cético sobre os perigos do Bayesianismo. De fato, o primeiro passo em qualquer processo judicial legítimo é de tentar encontrar a verdade do caso: Para assegurar de que os fatos em questão ocorreram ou não, e se as declarações relevantes se encaixam com ditos fatos, isto é, são verdadeiras pelo menos por primeira aproximação. Na lei, assim como na ciência e tecnologia, nós procuramos sólida episteme (ciência) e não mera doxa (opinião).

Além disso, no campo da ação humana há certamente muitos acidentes, mas não há nenhuma chance ou aleatoriedade irredutível do tipo que encontramos na mecânica quântica, química quântica, biologia molecular ou genética. Em particular, o conceito de acaso ou aleatoriedade não tem lugar na criminologia. As pessoas roubam ou não, assassinam ou não, e assim por diante: Não há nada aleatório sobre o crime, porque cada ação criminosa é o último elo em uma ou mais cadeias causais. Ora, acontece que nas ciências apenas estados e mudanças de estado (eventos) são atribuídos probabilidades. Além disso, muitas vezes tais probabilidades podem ser calculadas sem ambiguidade e medidas com precisão em vez de serem atribuídas arbitrariamente.

Por exemplo, os físicos calculam e medem a probabilidade de que uma determinada partícula de entrada seja desviada por um núcleo atômico alvo dentro de um determinado ângulo sólido durante uma única unidade de tempo. É verdade que a probabilidade também é utilizada nas ciências biossociais, como a epidemiologia e nas ciências sociais, como a sociologia. Assim, por exemplo, pode-se legitimamente falar de probabilidade de contágio, e da probabilidade de alguém subir ou descer uma hierarquia social por razões diferentes do mérito. Mas nesses casos, assim como na ciência natural, as probabilidades em questão são objetivas, não subjetivas, e são estimadas por frequências relativas observadas. Ou seja, as frequências de certos tipos podem ser usadas como indicadores de probabilidade.

Em suma, a interpretação da probabilidade empregada na ciência e tecnologia não é subjetiva ou bayesiana, mas objetiva ou realista. É considerado como uma medida de possibilidade objetiva, desordem objetiva, ou ambos – como quando se extrai uma carta de um baralho repetidamente embaralhado.

Ninguém na ciência, com exceção dos psicólogos e sociólogos que estudam a crença, está interessado em meras opiniões sobre fatos; E ninguém é ousado ou ingênuo o suficiente para atribuir probabilidades a dados científicos ou hipóteses científicas, como os Bayesianos fazem. Certamente, muitas vezes entregam-se a estimativas subjetivas de probabilidades objetivas, assim como um pode executar estimativas intuitivas de qualquer outra magnitude. No entanto, essas estimativas são extra teóricas e nunca pretendem substituir cálculos bem fundamentados ou medições precisas.

2. Quebra-cabeças de Monty Hall

Há toda uma série de problemas Monty Hall, também chamados de quebra cabeças de Marilyn Vos Savant. Todos alegadamente envolvem probabilidades. Aqui está o mais simples e mais conhecido deles. Há três portas idênticas em um quarto. Atrás de uma das portas há um prêmio para o indivíduo que escolher abrir aquela porta sem tentar nenhuma das outras duas. O problema é: Qual é a probabilidade de que o prêmio esteja por trás de uma determinada porta? A maioria das pessoas responderá sem hesitar: 1/3.

As pessoas que respondem dessa maneira não percebem que há dois problemas envolvidos aqui: adivinhar a probabilidade da presença do prêmio atrás de uma determinada porta, e adivinhar a probabilidade de abrir a porta certa. Enquanto o segundo problema é legítimo, o primeiro é um pseudoproblema, porque pressupõe que o prêmio tenha sido colocado ao acaso, enquanto na verdade a escolha da porta foi deliberada. E, mesmo se a porta fosse escolhida ao acaso, o acaso evaporou assim que o prêmio foi depositado.

Só o segundo problema, o de adivinhar a porta vencedora, é legítimo, porque a pessoa convidada a abrir uma porta a escolhe aleatoriamente, ao invés de à luz de qualquer informação privilegiada. Aqui a aleatoriedade reside na escolha, que é um processo cerebral, não na sala. Mas, mesmo neste caso, pode-se argumentar que, na verdade, o que está envolvido é a incerteza. Dignificar este estado mental com o nome de “probabilidade” é ilegítimo, porque não pertence a nenhum modelo estocástico na psicologia cognitiva.

O problema dos três prisioneiros é mais dramático, mas conceitualmente o mesmo. Três homens, Lucas, Marcos e Mateus, estão trancados em celas separadas. Eles estão esperando que seu juiz escolha dois deles para execução. Eles argumentam que cada um deles tem a probabilidade 1/3 de salvar seu pescoço. Marcos, o mais esperto dos três, pede ao carcereiro o nome de um dos três prisioneiros que certamente será executado. O carcereiro aceita, e informa que Lucas é um dos dois condenados. Marcos sente-se aliviado, porque acredita que sua chance aumentou de 1/3 para 1/2.

Marcos está certo? Não, porque o juiz já escolheu quem será condenado à morte, e não há nenhuma indicação de que ele fez isso de forma aleatória. Neste caso, então, há incerteza na mente de dois homens. Além disso, é verdade que a incerteza de Marcos diminuiu um pouco, embora não possamos determinar por quanto. Mas a aleatoriedade não está nem na situação objetiva nem nas mentes de nenhum dos personagens da tragédia. Portanto, não há mandado para invocar probabilidade neste caso.

3. Ignorância aprendida

Apesar de sua popularidade entre os filósofos, e sua multidão de fiéis entre os estatísticos, o Bayesianismo é uma visão minoritária na comunidade científica. A razão pela qual os cientistas têm de evitar o Bayesianismo é que, por ser subjetivista, convida arbitrariamente as atribuições de probabilidade a qualquer coisa – dificilmente um procedimento científico.

O Bayesianismo origina-se de um dogma ontológico e de duas grandes confusões. O dogma em questão é o determinismo clássico ou causalismo, tão brilhantemente descrito por Laplace há dois séculos, e certamente justificável em seu tempo. Esta é a tese de que tudo acontece de acordo com leis que, como a de Newton, têm um amplo domínio causal (ver Bunge, 1979). Se o causalismo fosse verdadeiro, o acaso seria de fato um nome para nossa ignorância das causas, de modo que um ser onisciente poderia dispensar o conceito de chance.

No entanto, as leis básicas da teoria quântica e da genética populacional são probabilísticas e não derivam de leis causais. Pelo contrário, muitas macro-leis são leis de médias, e podem assim serem deduzidas de micro-leis probabilísticas. A segunda lei da termodinâmica clássica é um caso disso; outra é a lei do decaimento exponencial de uma amostra de material radioativo. Tanto para o erro na raiz da interpretação subjetivista da probabilidade. Vejamos agora as confusões que a acompanham.

Uma primeira confusão é aquela entre proposições (ou declarações) e os fatos a que se referem. Suponha, por exemplo, que V designe uma variável aleatória, como o número de pontos marcados em um lance de dado. Além disso, chamar P (V = v) a probabilidade de que, em uma determinada ocasião, a variável V assume o valor particular v, como o ás. A proposição “P (V = v) = 1/6” envolve a proposição “V = v”, mas não deve ser lida como a probabilidade dessa proposição, uma vez que tal expressão não faz nenhum sentido claro. O jogador sabe que a proposição “P (V = ás) = 1/6” indica a probabilidade do fato de obter um ás ao jogar um copo de dados bem chacoalhado. Ele está interessado no resultado de um processo real caracterizado pela desordem objetiva – a resultante de agitação vigorosa e repetida.

Uma segunda grande fonte de Bayesianismo é a confusão do acaso objetivo com a incerteza subjetiva. Trata-se de uma confusão entre uma categoria ontológica e uma psicológica (e epistemológica). Com certeza, essa confusão é bastante natural, porque a indeterminação objetiva implica incerteza subjetiva – embora não o contrário. Por exemplo, ao agitar vigorosamente um copo de dados, cada um dos seus seis lados adquire a mesma chance de surgir quando o dado é lançado. No entanto, uma vez que o dado é lançado, a determinação substituiu a indeterminação, enquanto a incerteza subjetiva permanece enquanto não olharmos para o dado. Bayesianos não têm o direito de dizer que a probabilidade de que eles vejam um ás é 1/6, porque o processo aleatório que culminou neste fato terminou: alea jacta est. Se um ás é o que surgiu, o jogador é permitido olhar, e sua visão é normal, ele verá um ás não importando suas expectativas.

Além disso, o processo mental do jogador é bem diferente do processo físico aleatório que ela desencadeia ao jogar dados. Tanto assim, que o jogador que ignora as leis do acaso é obrigado a formar expectativas irracionais, como a popular falácia do apostador. (“O próximo lance deve ser um ás, já que nenhum ás ocorreu nos últimos cinco lances”). Ou seja, nossas expectativas podem não refletir o acaso objetivo. Se o fizessem, nem os casinos nem as loterias seriam lucrativos. A única maneira de derrotar o acaso é trapaceando. Tanto assim, que as pessoas racionais se abstenham de jogar roleta, ou qualquer outro jogo de azar, se suspeitarem que os dispositivos envolvidos foram adulterados de modo a violar as leis de probabilidade. Em suma, probabilidade se, e somente se, a chance for objetiva.

4. Probabilidade como crença

Examinemos agora a afirmação bayesiana de que as probabilidades são credibilidades, ou intensidades de crença. Esta é uma questão empírica, portanto não pode ser resolvida a priori – como os subjetivistas fazem. Vamos, portanto, perguntar psicólogos cognitivos se as pessoas realmente pensam de acordo com o referido cálculo quando o raciocinam sobre questões incertas. Os muitos experimentos de Daniel Kahneman e seus alunos têm demonstrado conclusivamente que nossos julgamentos subjetivos de verossimilhança e plausibilidade são muitas vezes incorretos e não atendem aos axiomas do cálculo de probabilidade (Kahneman et al., 1982).

Para começar, ao considerar um processo de ramificação, como uma filogenia ou uma árvore de decisão, raramente há dados suficientes para incluir todos as possíveis bifurcações – uma condição para garantir que a soma das probabilidades sobre todos os ramos é igual à unidade. Em segundo lugar, tendemos a exagerar as probabilidades de certos eventos extremamente improváveis, como o de ganhar na loteria. Terceiro, como observou Venn (1962) há mais de um século, o medo, a cobiça, a ilusão, a superstição, a forte emoção e a associação com experiências prazerosas ou dolorosas estão entre os fatores que distorcem nossos julgamentos da probabilidade objetiva e da frequência real de um evento. Por exemplo, pode-se “provar” a ocorrência de qualquer fenômeno paranormal atribuindo uma alta probabilidade prévia de acreditar nele.

Finalmente, considere o seguinte contraexemplo à hipótese de que as crenças satisfazem as leis de probabilidade. Uma dessas leis é “P (A & B) £ P (A), P (B)”. Tal que A = “Liberdade é boa”, e B = “Igualdade é boa”. Libertários juram por A, igualitaristas por B, nenhum por ambos. Na minha opinião, nem a liberdade nem a igualdade são por si só um bem social, ou mesmo viável, porque a liberdade é impossível entre desiguais, e a igualdade forçada amortece a liberdade. Mas é possível argumentar que a combinação da liberdade com a igualdade é viável e desejável (Bunge, 2009). Portanto, se tivéssemos uma teoria plausível de crenças, ela incluiria o duo da desigualdade probabilística, a saber, C (A & B) ³ C (A), C (B), onde C significa credibilidade ou força de crença. Em suma, Percepção de plausibilidade ≠ Probabilidade objetiva. Em outras palavras, Probabilidade ≠ Grau de crença racional.

5. Probabilidades prévias são inescrutáveis

Uma condição para a aplicação legítima do teorema de Bayes é que três das quatro probabilidades ocorridas no teorema sejam conhecidas. Assim, quando as probabilidades prévias P (A) e P (B) são desconhecidas, como é o caso quando A = hipótese h e B = evidência e, escrevendo P (h | e) e P (e | h) em seus termos, equivale a desenhar rabiscos. E, no entanto, é assim que o teorema de Bayes é usado tanto na estatística bayesiana como na lógica indutiva.

Em instância, ao estimar a probabilidade de um evento, ou a plausibilidade de uma conjectura, o Bayesiano consulta um painel de especialistas. Ou seja, ele busca “uma visão em consenso da opinião informada”, da mesma forma como se procede na vida cotidiana com relação aos assuntos do dia a dia- com a diferença de que o Bayesiano atribui números às forças de crença (ver, por exemplo, Press 1989).

Verdade, os autodenominados Bayesianos objetivistas equiparam Pr (h|e) à frequência correspondente – por exemplo, que um teste clínico positivo é evidência de uma certa doença; mas constituem as outras “probabilidades”, em particular P (h). Além disso, ao equiparar certas probabilidades com frequências, elas violam o dogma bayesiano de que as probabilidades são credenciais.

Priores desconhecidos, que devem ser estipulados arbitrariamente, não preocupam mais o bayesiano do que os projetos inescrutáveis de Deus preocupam o teólogo. Assim, Lindley (1976), um dos líderes da escola bayesiana, sustenta que essa dificuldade tem sido “grosseiramente exagerada”. E ele acrescenta: “Muitas vezes me perguntam se o método [Bayesiano] dá a resposta correta: ou, mais particularmente, como você sabe se você tem o priori certo [probabilidade]. Minha resposta é que eu não sei o que significa “certo” neste contexto. A teoria bayesiana é sobre a coerência, não sobre o certo ou o errado “(op. Cit: 359). Assim, o bayesiano, assim como o imperialista lógico que só se preocupa com a coerência dos argumentos, encaixa-se com o raciocínio louco.

6. Bayesianismo pode ser desastroso

Sem surpresas, o Bayesianismo pode ter consequências catastróficas. Lembremos um exemplo famoso, que diz respeito à avaliação de riscos. Em 1986, quando o ônibus espacial Challenger explodiu, a comissão de inquérito descobriu que os gerentes do projeto haviam estimado que a “probabilidade” de falha era de um milésimo da prevista pelos engenheiros. Mas o Comitê não se preocupou em perguntar como esses números foram gerados: não questionou a ideia de que, como não havia precedentes de falha nas missões espaciais, os especialistas podiam atribuir números ás suas intuições.

Apenas um membro do Comitê, o famoso físico Richard Feynman, ousou afirmar que a avaliação de risco excessivamente otimista dos gerentes era devido à sua preocupação com as relações públicas. Em todo caso, ambos os números em questão, o 1/100 dos engenheiros, e 1/100.000 dos gerentes, eram “probabilidades subjetivas”: representavam os graus de crença dos indivíduos em vez da confiabilidade do artefato. E, no entanto, deve ser óbvio que o malabarismo com as probabilidades é inadequado no caso da falha dos componentes de uma máquina, porque esta é uma cadeia causal, não aleatória – como uma cadeia de Markov, na qual cada uma tem uma probabilidade objetiva que depende apenas da ligação anterior. Como é bem sabido, o próprio Feynman encontrou uma das ligações defeituosas da Challenger.

Em geral, os desastres – do travamento de computador à morte precoce, da bancarrota à extinção de biospécies, do furacão ao tsunami, da epidemia à guerra e do roubo a banco ao assassinato – são eventos não aleatórios, portanto não podem ser contabilizados em termos probabilísticos. É verdade que a extinção das espécies e o declínio dos ecossistemas têm sido frequentemente modelados assumindo que esses processos são aleatórios. Mas eles não são. De fato, as variáveis ecológicas dominantes são não-aleatórias: Pense no clima, raridade das espécies, tamanho do corpo e presença ou ausência de carnívoros, espécies-chave (como peixes-estrela) e invasores agressivos (como capim-elefante). Portanto, esses modelos estocásticos são irrealistas e, consequentemente são ferramentas enganosas para projetar políticas de proteção ambiental. A moral é que a probabilidade sem aleatoriedade pode ser perigosa para o ambiente. (Veja exemplos de riscos de saúde do Bayesianismo em Bunge, 2006).

7. Julgamento por números

Frases como “probabilidade de culpa”, “probabilidade de reincidência”, “equilíbrio de probabilidades” e “probabilidade de um veredito justo” são bastante comuns no jargão jurídico moderno. Isto pode ser devido em parte à influência saudável do ceticismo que acompanha o empirismo britânico (particularmente escocês). Suponho que as frases em questão são legítimas, desde que a palavra “probabilidade” seja tomada em seu sentido informal de linguagem, mas que convida problemas quando interpretados como designando o conceito elucidado pela teoria matemática da probabilidade. (O mesmo vale para os equivalentes francês e alemão de ‘provável’.) Sugiro que, para evitar problemas, se deve falar de verossimilhança no caso dos fatos, e de plausibilidade no de hipóteses. Vejamos mais de perto esta questão, que não é meramente uma questão terminológica.

Considere a sentença “Ele provavelmente cometeu o crime”. Afirmo que o advérbio não deve ser tomado literalmente, no sentido do cálculo da probabilidade, porque os crimes são cometidos ou não cometidos: são resultados de ações deliberadas, não de processos aleatórios. (Isto acontece mesmo que o criminoso deixe o dado decidir por ele.) Portanto, a frase em questão deve ser substituída por esta: “É verossímil que ele cometeu o crime”. E, claro, nenhuma tentativa de quantificar essa verossimilhança deve ser feita. O máximo que podemos fazer é adicionar a informação estatística de que crimes de um determinado tipo ocorrem com tal e tal frequência entre pessoas com as mesmas características.

O mesmo acontece, é claro, para as sentenças do formulário «Dada essa (ou à luz dessa) prova, é provável que o réu tenha cometido o crime». Basta dizer que a evidência em questão apoia a suposição (ou hipótese) de que o indivíduo em questão é culpado. E não tente atribuir um número ao peso da evidência, porque as escalas da justiça não são precisas. Escrever fórmulas como “P(h|e)=0.75” é na melhor das hipóteses um desperdício de tempo.

O que às vezes pode ser feito é medir a frequência relativa de ações de um certo tipo. Por exemplo, sabe-se que a frequência das infrações penais depende da idade. Esta distribuição aumenta a partir da infância, picos em cerca de 17 anos, e depois decai até um platô. As causas da delinquência juvenil são múltiplas, entre elas a pobreza, a maior liberdade e os impulsos mais intensos dos adolescentes, juntamente com a maturação comparativamente lenta do córtex pré-frontal (ver, por exemplo, Hawkins, 1996, Maguire et al. 1994; Robinson 2004;Wikström e Sampson, 2006).

Cuidado: Esses dados não podem ser usados para construir a probabilidade prévia de que um adolescente cometa um crime, porque o crime não é aleatório. Da mesma forma, o fato de que quase metade da população mundial é asiática não é motivo para esperar que a probabilidade de que um casal islandês dê à luz uma criança asiática seja metade. As estatísticas nos dão regularidades coletivas, não disposições individuais.

8. Conclusão

Em conclusão, as estatísticas bayesianas e a lógica indutiva são triplamente erradas: porque atribuem probabilidades a declarações; porque concebem as probabilidades como subjetivas; e porque invocam probabilidades na ausência de aleatoriedade.

A contemplação do umbigo não nos ajuda a explorar o mundo real. Também não invoca números arbitrários: trata-se apenas de um disfarce de ignorância. A experiência subjetiva é um assunto para a investigação científica (psicológica), não um substituto para ela. E o subjetivismo, seja de Berkeley, Kant, Fichte, Husserl ou Bayesiana, é uma marca de anticiência ou pseudociência.

Ignorância aprendida ainda é ignorância. Em particular, o diagnóstico médico com a ajuda de números inventados não é mais seguro do que sem eles; E julgamento por números não é mais justo do que julgamento por ordália ou por combate. Não apostarás com a vida, a justiça ou a verdade.

Referências

• Bunge, Mario. 1951. What is chance? Science & Society 15: 209–231.
• Bunge, Mario. 1955. Strife about complementarity. British Journal for the Philosophy of Science 6: 1–12: 6: 141–154
• Bunge, Mario. 1976. Possibility and probability. In Foundations of probability theory, statistical inference, and statistical theories of science, vol. 3, ed. W.L. Harper and C.A. Hooker, 17–34. Boston: D. Reidel.
• Bunge, Mario. 1979 [1950]. Causality: The place of the causal principle in modern science. New York: Dover.
• Bunge, Mario. 1981. Four concepts of probability. Applied Mathematical Modelling 5: 306–312.
• Bunge, Mario. 1988. Two faces and three masks of probability. In Probability in the sciences, ed. E. Agazzi, 27–50. Dordrecht: Reidel.
• Bunge, Mario. 2003. Emergence and convergence: qualitative novelty and the unity of science. Toronto: University of Toronto Press.
• Bunge, Mario. 2006. Chasing reality: Strife over realism. Toronto: University of Toronto Press.
• Bunge, Mario. 2008. Bayesianism: Science or pseudoscience? International Review of Victimology 15: 169–182.
• Bunge, Mario. 2009. Political philosophy. New Brunswick: Transaction.
• Bunge, Mario. 2010. Matter and mind, Boston studies in the philosophy of science, vol. 287. Dordrecht/Heidelberg/London/New York: Springer.
• Carnap, Rudolf. 1950. Logical foundations of probability. Chicago: University of Chicago Press.
• De Finetti, Bruno. 1962. Does it make sense to speak of ‘good probability appraisers’? In The scientist speculates: an anthology of partly-baked ideas, ed. I.J. Good. London: Heinemann.
• De Finetti, Bruno. 1972. Probability, induction, and statistics. New York: Wiley.
• Eddy, Charles. 1982. Probabilistic reasoning in clinical medicine: Problems and opportunities. In Judgment under uncertainty: Heuristics and biases, ed. D. Kahneman, P. Slovic, and A. Tversky, 249–267. New York: Cambridge University Press.
• Feller, William. 1968. An introduction to probability theory and its applications, vol. 1, 3rd ed. New York: Wiley.
• Fréchet, Maurice. 1955 [1946]. Les de fi nitions courantes de la probabilité. In Les mathématiques et le concret , pp. 157–204. Paris: Presses Universitaires de France.
• Hawkins, J. David (ed.). 1996. Delinquency and crime: Current theories. Cambridge, UK: Cambridge University Press.
• Humphreys, Paul. 1985. Why propensities cannot be probabilities. Philosophical Review 94: 557–570.
• Jeffreys, Harold. 1975 [1939]. Scienti fi c inference, 3d ed. Cambridge, UK: Cambridge University Press.
• Kahneman, Daniel, Paul Slovic, and Amos Tversky (eds.). 1982. Judgment under uncertainty: Heuristic and biases. Cambridge, UK: Cambridge University Press.
• Keynes, John Maynard. 1957 [1921]. A treatise on probability. London: Macmillan.
• Lahey, Benjamin B., Terrie E. Mof fi tt, and Avshalom Caspi (eds.). 2003. Causes of conduct disorder and juvenile delinquency, 118–148. New York: The Guilford Press.
• Lindley, Dennis V. 1976. Bayesian statistics. In Foundations of probability theory, statistical inference, and statistical theories of science, vol. 2, ed. W.L. Harper and C.A. Hooker, 353–362. Dordrecht/ Boston: D. Reidel.
• Maguire, Mike, Rod Morgan, and Robert Reiner (eds.). 1994. The oxford handbook of criminology. Oxford: Clarendon.
• Press, S. James. 1989. Bayesian statistics: Principles, models, and applications. New York: Wiley.
• Robinson, Matthew B. 2004. Why crime? An integrated systems theory of antisocial behavior. Upper Saddle River: Pearson/Prentice Hall.
• Savage, L. James. 1954. The foundations of statistics. New York: Wiley.
• Venn, John. 1962 [1866]. The logic of chance. London: Chelsea Publications Co.
• Wikström, Per-Olov, and Robert J. Sampson (eds.). 2006. Crime and Its explanation: Contexts, mechanisms and development. Cambridge, UK: Cambridge University Press.