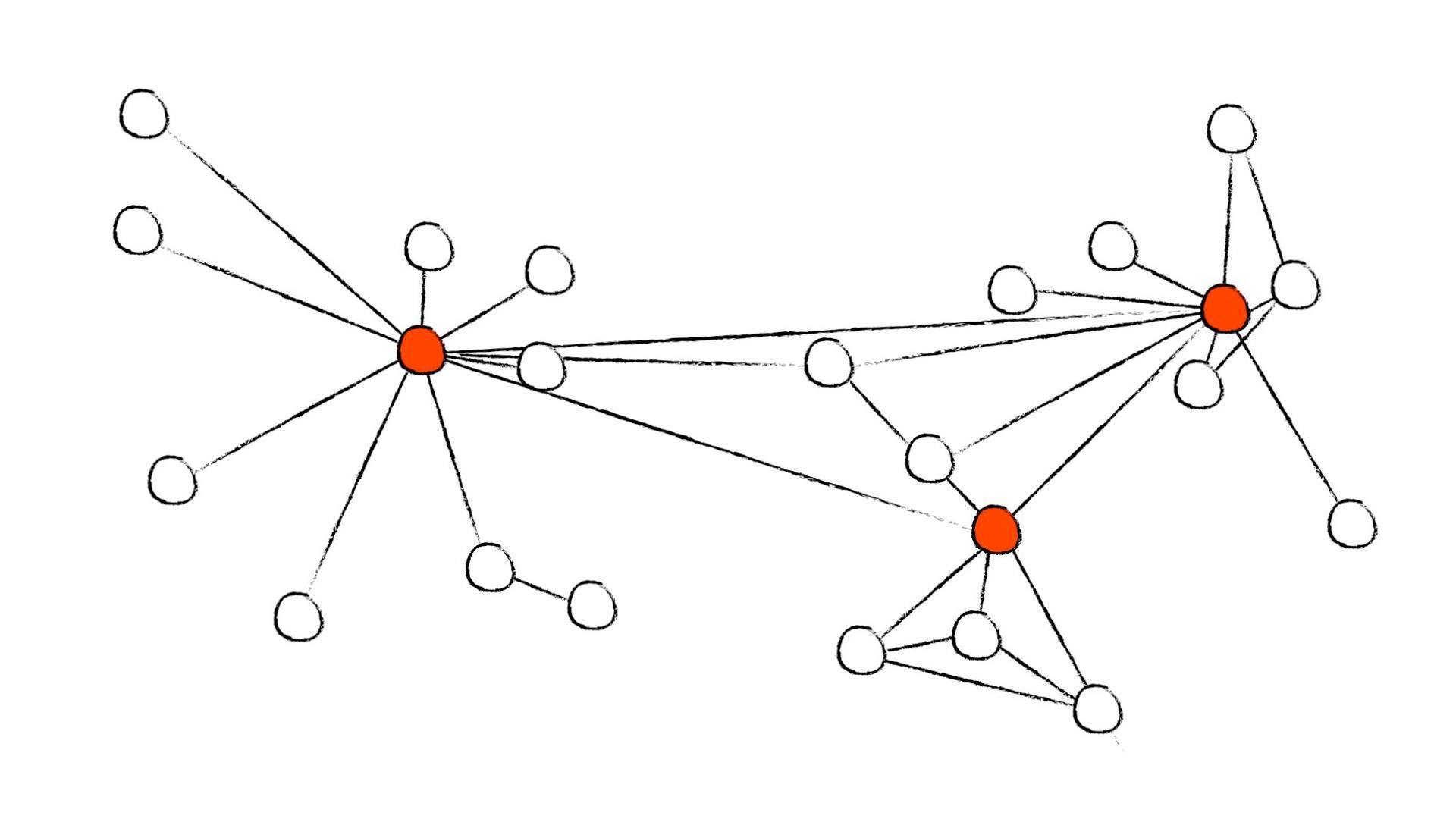
Você acaba de conhecer uma pessoa. Aí papo vai, papo vem, e vocês descobrem que têm um conhecido em comum. “Ah, que mundo pequeno!”, um diz.
Terá sido mera coincidência? Será um plano dos illuminatis? Ou aliens?
Tenho a impressão de que você, leitor do UR, está se perguntando: afinal, tem algo de científico nesse ditado popular de “mundo pequeno”?
Efeito Small World
Nossa história tem início lá na década em que os Beatles começaram – e terminaram. Nos anos sessenta, o sociólogo Stanley Milgram estava interessado numa hipótese em aberto na comunidade científica daquele tempo. A hipótese era de que a popular frase “Que mundo pequeno!” tinha algo de científico. Esta sensação de mundo pequeno, presente no senso comum, é tema de estudo sério desde então. Nesta década, Milgram conseguiu resultados que ecoariam até os dias de hoje – e não só na Sociologia, como também na Biologia, Matemática, Economia e Ciências da Computação.
Milgram estava interessado na hipótese de que o mundo, visto como uma rede baseada em fenômenos sociológicos, era pequeno. Isso no sentido de que qualquer par de pessoas no planeta poderia se conectar através de amigos, amigos de amigos e assim por diante, com poucos intermediários. Mesmo que eu não te conheça, devo conhecer alguém, que conhece alguém e que conhece você. A principal pergunta de MIlgram era: quantos “alguém’s” há no caminho?
Mais precisamente, ele queria o número médio de links pra conectar duas pessoas. Se A conhece B, há um link entre A e B.
Pra isso, Milgram fez o que hoje se chama Método Small World, que consiste no seguinte: ele deu, aleatoriamente, cartas a algumas centenas de pessoas de Boston e Omaha (cidades dos EUA) – que distam cerca de 2.700 km. As cartas deviam ser enviadas a um corretor da bolsa de valores de Sharon, Massachusetts, que trabalhou em Boston. O receptor só podia passar a carta a alguém que pudesse conhecer o alvo ou que achasse estar mais próximo de alcançar o alvo que ele próprio.
Perguntando às pessoas quantos passos levaria uma carta de um lugar a outro (possivelmente de Boston a Nebraska), as estimativas estavam na casa das centenas. O resultado, porém, foi de que as cartas que chegaram levaram em média 6 passos até o destino. Este resultado surpreendeu os estudiosos da época.
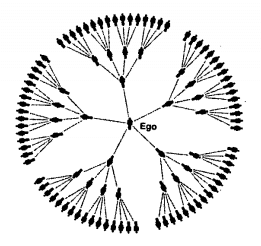
Com alguma malícia matemática, você poderá estranhar a surpresa. Façamos um experimento mental. Suponha que eu tenha 100 conhecidos e cada um deles possui também 100 conhecidos. Com um grau de separação, conecto 100 pessoas e com dois alcanço 10.000 (100×100). Com grau de separação três, chego a 1.000.000 (um milhão de pessoas). Com quatro, cem milhões. Já com cinco, conheço todas as pessoas do planeta, “MUAHAHA!”. Então é óbvio que o mundo é pequeno!
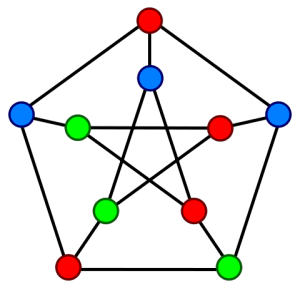
No entanto, se você tem uma certa inclinação às ciências humanas, deve ter percebido uma falha no experimento mental que fizemos. Se pergunte: “quem são os 10 melhores amigos dos meus 10 melhores amigos?”, as chances de nomes comuns nessas listas são enormes. O mesmo se aplica aos conhecidos, porque vários dos conhecidos, digamos, se conhecem… Esta é uma propriedade que chamamos de coeficiente de aglomeração (clustering), que diz que se A é amigo de B e B é amigo de C, grandes são as chances de A ser (ou se tornar) amigo de C. Isso faz sentido, né? Lembre de como conheceu seus amigos e verá que vários foram por meio de amigos/conhecidos em comum entre vocês. A figura a seguir ilustra melhor o que é uma rede social.
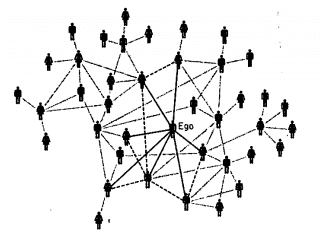
As “panelinhas” são naturais e tendem a caracterizar os grupos. Com isso, a conexão entre grupos é relativamente baixa (do contrário, seriam um grupo só e não um par). Isso significa que quanto mais seus amigos se conhecem, menor utilidade eles têm pra enviar sua mensagem a um desconhecido teu. Então, se você precisar de um emprego, tente não depender só dos melhores amigos.
Por um lado, o mundo é altamente clusterizado (vários de meus amigos são também amigos entre eles). Por outro lado, na média, a distância entre qualquer par de pessoas é muito pequena. Parafraseando John Guare, em sua peça “Six degrees of separation”, seis graus de separação entre você e qualquer outra pessoa nesse planeta – seja ela um nobel de Física ou até presidente dos Estados Unidos… E não é só pra grandes nomes, é qualquer um. Você está conectado a um esquimó por seis apertos de mão! Reflita um pouco, isso é profundo…
O número 6 não tem nada de especial, poderia ser outro número, pois aqui o resultado genérico tem mais relevância. A afirmação do efeito Small World é a de que não importa o que a pessoa de origem e a de destino tenham em comum, a distância social continua sendo minúscula frente ao número de pessoas.
Modelo Watts-Strogatz
A ciência das redes tem como base a Teoria dos Grafos, que é um modelo matemático pra representar relações entre pares de coisas.
Há várias classes de grafos, uma delas é o que se chama de grafo aleatório.
Grafos aleatórios são irrealistas, pois não possuem estrutura local. Já vimos que a tendência numa rede de conhecidos é de formar triângulos – se A é amigo de B e B é amigo de C, a chance de A se tornar amigo de C é grande. Num grafo aleatório, esta chance seria a mesma para qualquer par de vértices (pessoas, no caso), por isso ele não condiz com as redes sociais reais.
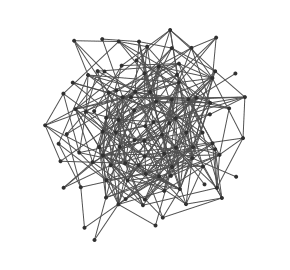
O coeficiente de aglomeração C é que mede a chance de fechar triângulos (e, consequentemente, a estrutura local). Em grafos aleatórios, C vale p, onde p é a probabilidade de conexão entre dois nós. Isto diz que a probabilidade de conexão entre vértices aleatórios é a mesma do que de vértices com vários vizinhos em comum.
Em muitas redes reais, C é muito maior que p, mostrando um efeito “vizinhança”. Para melhor representar redes reais, precisamos dum modelo onde as distâncias médias sejam pequenas, sem perder o fator “vizinhança”, ou seja, mantendo alto o coeficiente de aglomeração C.
Foi em 1998 que Duncan James Watts e Steven Strogatz propuseram um modelo simples para reproduzir as características citadas no parágrafo anterior. A intenção deles, como diz o próprio Watts em seu livro Six Degrees, era capturar quatro elementos no modelo. O primeiro era de que redes sociais consistiam em muitos grupos, com muitas conexões internas. O segundo era de que redes sociais não eram estáticas, pois novas relações são feitas e outras deixam de existir com o passar do tempo. O terceiro era de que as relações não têm, necessariamente, a mesma probabilidade de existir, isto é, o contexto influencia nas futuras relações. O quarto e último elemento consistia no fato de que nossas decisões são derivadas de nossas preferências e características (quando as tomamos), estas decisões nos levam a conhecer novas pessoas.
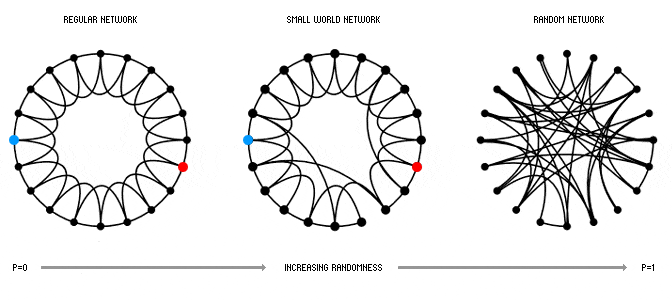
Ao saber que já existiam estudos sobre o fenômeno Small World, eles passaram a tentar descobrir o que causava esse efeito. A pergunta da vez era: qual é o modelo mais simples capaz de reproduzir o efeito Small World? Num extremo, temos uma rede regular, que é uma rede com simetria de conexões. No outro, uma rede aleatória (que não tem esse nome à toa). Uma rede regular não é um modelo apropriado pra ver relações de pessoas, afinal, não temos nem a mesma quantidade de amigos. Uma rede aleatória pode até parecer mais real que uma rede totalmente simétrica, mas dizer que ela é boa para a modelagem seria ignorar muito do que a sociologia já trouxe à luz sobre as forças sociais que atuam nestes sistemas – os triângulos, de novo! Então, o modelo teria de estar entre a organização e a bagunça.
Vamos chamar de L a distância média entre vértices. Aqui, link é sinônimo de aresta. A ideia básica do modelo é a de que, por um lado, as redes aleatórias têm baixo L e baixo C; por outro lado, redes regulares possuem alto L e alto C. Eles buscaram um regime intermediário entre estes dois extremos. O algoritmo também é simples. Cria-se um grafo regular e, para cada vértice, é escolhida uma aresta aleatória (que ainda não foi escolhida) e ela é apontada aleatoriamente pra outro vértice, ligando o vértice em questão a outro. Ao fazer isso, para valores baixos de p, obtém-se um modelo com C alto e L baixo.
O gráfico abaixo ilustra o resultado do trabalho de Watts e Strogatz, publicado na Nature. Do compromisso entre alto coeficiente de aglomeração e baixa distância média (ordem e desordem), foram descobertas as redes Small World.
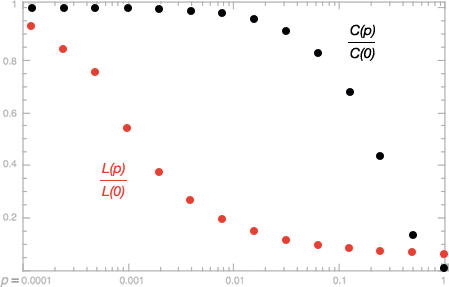
Vértices vizinhos diferem em poucas conexões e isso se mantém mesmo após os rearranjos das conexões, tendo só um efeito local, de modo a não influenciar na estrutura da rede como um todo. O coeficiente de aglomeração diminui com as realocações, mas diminui lentamente.
Já a distância média cai drasticamente em cada rearranjo. Isso faz sentido, pois uma realocação não só vai estar diminuindo a distância entre os dois vértices relacionados a ela, como também a qualquer par de vértices cujo caminho de um ao outro passe por esta aresta rearranjada, tendo efeito na estrutura da rede. Um resultado surpreendente obtido por Watts e Strogatz foi de que, na média, o L da rede após cinco realocações cai pela metade, independentemente do tamanho da rede.
O modelo Watts-Strogatz reproduz as principais características de muitas redes sociais.
Pra facilitar, imagine várias pessoas num estádio, assistindo um jogo de futebol nos anos 80. Elas só conseguem falar com pessoas próximas, pois o barulho da multidão é grande demais pra que consigam falar com alguém do outro lado do estádio.
No entanto, algumas pessoas recebem um rádio pra falar com um torcedor aleatório presente, também com um rádio. Agora, essa galera tem muito mais facilidade de contatar pessoas na arquibancada do estádio do que alguém sem rádio. O rearranjo das arestas é quando são introduzidos os rádios.
Small World em outras redes
Watts e Strogatz passaram a buscar dados de redes reais pra verificar se suas previsões condiziam com a realidade.
Em 1994, um jogo chamado Kevin Bacon Game passou a ficar popular (sim, o ator Kevin Bacon). Atores são os vértices da rede. Há uma aresta ligando dois atores, se eles participaram em ao menos um filme juntos. Essa rede não se restringe a Hollywood, o filme pode ter sido feito em qualquer lugar e em qualquer época. De acordo com o IMDB (Internet Movie Database), entre os anos de 1898 e 2000, atuaram em filmes cerca de 500 mil pessoas, totalizando algo em torno de 200 mil filmes. Se você atuou num filme com Kevin Bacon, seu número Bacon é 1. Se atuou com alguém que atuou com ele, seu número Bacon é 2, e assim por diante. O objetivo do jogo é determinar o menor número Bacon possível de um certo ator até o Kevin.
A tabela a seguir mostra a distribuição de atores de acordo com o número Bacon.
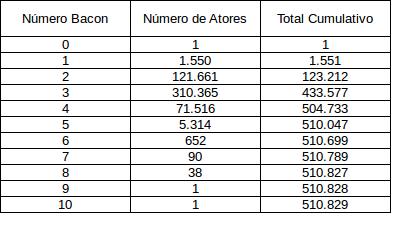
Quase 90% dos atores na base de dados tinham um número Bacon finito, isto é, estavam conectados ao ator. Isso quer dizer que essa rede tinha um componente enorme (componente é um “pedaço” da rede que está todo interligado).
Podemos ver que mais de 500 mil atores podem ser conectados a Kevin Bacon por poucos filmes. Você pode argumentar que o resultado é esse porque foi escolhido um ator influente como referência para a distância. Watts e Strogatz sabiam disso e fizeram a mesma análise a partir de todos os outros atores do componente gigante. O resultado, com as palavras do próprio Watts foi de que “em um mundo com centenas de milhares de indivíduos, todo ator poderia ser conectado a qualquer outro ator numa média de menos de quatro passos”. Sem nenhuma dúvida, esta era uma rede Small World.
As redes Small Worlds estão por todas as partes. Numa rede alimentar, as espécies estão, em média, a dois graus de separação umas das outras. Moléculas nas células são separadas por três reações químicas, na média. Na linguagem humana, 3 links conectam, em média, palavras que aparecem várias vezes na mesma sentença – numa rede com 470 mil palavras! Cientistas das mais diversas áreas de atuação estão separados por entre quatro e seis coautorias. Neurônios duma espécie muito usada por neurocientistas (C. elegans) têm uma distância próxima de 14 sinapses uns dos outros. A Internet (que é a conexão física entre roteadores) tem 10 graus de separação entre quaisquer dispositivos dela. Páginas de toda a Web, na virada do milênio, estavam a uma distância média de 19 cliques.
Por que me importar?
Afinal, por que deveríamos nos importar com o efeito Small World? Como já foi dito, o primeiro registro desse efeito se deu numa rede social (que envolve pessoas). Redes Small World são muito importantes em comunicações, e grande parte da comunicação humana se dá diretamente – famoso boca-a-boca, ainda que virtual. O espalhamento de notícias, piadas, rumores e, talvez mais importante, doenças se dá de pessoa pra pessoa. A estrutura da rede influencia na rapidez de propagação, que pode ditar, por exemplo, nosso futuro numa epidemia.
Espero que esse papo tenha te conectado à Teoria das Redes. Se interessou? Entre em contato!
Qualquer dúvida, estou à disposição pra tentar ajudar.
Referências
WATTS, Duncan J.; STROGATZ, Steven H.. Collective dynamics of ‘small-world’ networks. Ithaca, New York: Nature, 1998. 3 p. Department Of Theoretical And Applied Mechanics, Kimball Hall, Cornell University. Disponível em: <http://www.nature.com/nature/journal/v393/n6684/abs/393440a0.html>. Acesso em: 22 jun. 2016.
DALLAQUA, Caio. Origem da Teoria dos Grafos: As 7 Pontes de Konigsberg. São Paulo: Universo Racionalista, 2016. Disponível em: <http://www.universoracionalista.org/origem-da-teoria-dos-grafos-as-7-pontes-de-konigsberg/>. Acesso em: 02 ago. 2016.
MILGRAM, Stanley. The Small-World Problem. Boston: Psychology Today, 1967. 7 p. Disponível em: <http://measure.igpp.ucla.edu/GK12-SEE-LA/Lesson_Files_09/Tina_Wey/TW_social_networks_Milgram_1967_small_world_problem.pdf>. Acesso em: 22 jun. 2016.
BARABÁSI, Albert-lászló. Linked: How Everything Is Connected to Everything Else and What It Means for Business, Science, and Everyday Life. Cambridge, Massachusetts: Plume, 2003. 281 p.
WATTS, Duncan J.. Small Worlds: The Dynamics of Networks between Order and Randomness. Princeton, New Jersey: Princeton University Press, 1999. 257 p. (Princeton Studies in Complexity).
ALBERT, Réka; BARABÁSI, Albert-lászló. Statistical Mechanics of Complex Networks. Minneapolis, Minnesota: Reviews Of Modern Physics, 2002. 51 p. Disponível em: <https://arxiv.org/pdf/cond-mat/0106096v1.pdf>. Acesso em: 11 jul. 2016.
NEWMAN, M. E. J.. Models of the Small World: A Review. Santa Fe: Journal Of Statistical Physics, 2000. 9 p. Disponível em: <http://link.springer.com/article/10.1023/A:1026485807148>. Acesso em: 11 jul. 2016.
CANCHO, Ramon Ferrer I; SOLÉ, Richard V.. The small world of human language. Londres: Proceedings Of The Royal Society B, 2001. Disponível em: <http://rspb.royalsocietypublishing.org/content/268/1482/2261.short>. Acesso em: 12 jul. 2016.
WATTS, Duncan J.. Six Degrees: The Science of a Connected Age. New York City: W. W. Norton & Company; Reprint Edition, 2004. 384 p.
FRANCO, Augusto de. REDES COMPLEXAS: DA INTERNET ÀS REDES SOCIAIS. : Escola de Redes, 2009. Disponível em: <http://escoladeredes.net/profiles/blogs/redes-complexas-da-internet-as>. Acesso em: 04 ago. 2016.
SEIS GRAUS DE SEPARAÇÃO. .: Nerdologia, 2014. (7 min.), son., color. Disponível em: <https://www.youtube.com/watch?v=YMI3CrChwSk>. Acesso em: 17 jul. 2016.
SEIS Graus de Separação (Documentário-2008). .: Revolução Científica, 2013. (47 min.), son., color. Disponível em: <https://www.youtube.com/watch?v=BQ7UDWn_uws>. Acesso em: 25 jul. 2016.
O PODER dos Seis Graus. .: Escola de Redes, 2011. (18 min.), son., color. Disponível em: <https://www.youtube.com/watch?v=gfrNfNkylbk>. Acesso em: 18 jul. 2016.
WINKLERPRINS, Lukas. Networks & Synchronicity. : Http://ltwp.net/, 2012. Disponível em: <http://ltwp.net/networks/>. Acesso em: 06 ago. 2016.