Por Ethan Siegel
Publicado na Forbes
Quando se trata de compreender o universo, há algumas coisas que todo mundo já ouviu falar: gato de Schrödinger, o paradoxos dos gêmeos e E = MC². Mas, apesar de estar triunfando por mais de 100 anos, a relatividade geral – a maior conquista de Einstein – é em grande parte misteriosa para todos, desde público em geral até estudantes de graduação e pós-graduação em física. Para esta semana no Pergunte ao Ethan, Katia Moskovtich, perguntou:
Você poderia um dia escrever uma história explicando a um leigo o que é a métrica na relatividade geral?
Antes de chegarmos à “métrica”, vamos começar no início, e falar sobre como conceituamos o universo, em primeiro lugar.
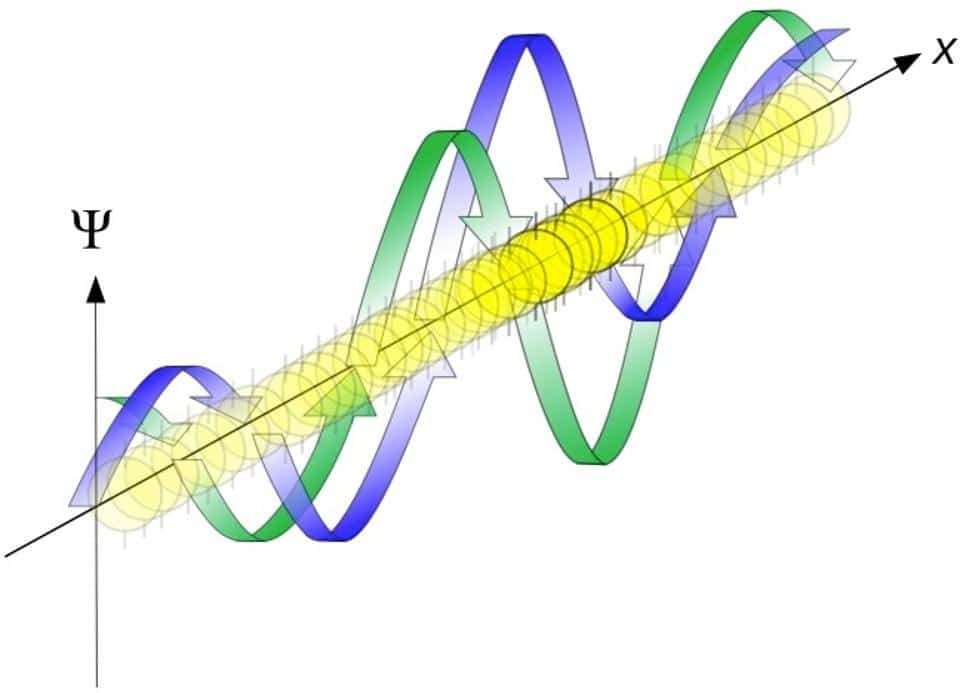
Em um nível fundamental, o universo é composto de quanta – entidades com propriedades físicas como massa, carga, momentum, etc. – que podem interagir uns com os outros. Um quantum pode ser uma partícula, uma onda ou qualquer coisa em algum estado intermediário, dependendo de como você olha para ele. Dois ou mais quanta podem se unir para construir estruturas complexas como prótons, átomos, moléculas ou seres humanos. A mecânica quântica pode ser relativamente nova, fundada no início do século XX, mas a ideia de que o universo é feito de entidades indivisíveis que se interagem umas com as outras remonta a mais de 2000 anos, ao menos em Demócrito de Abdera.
Mas não importa do que o universo é feito, as coisas que o compõem precisam de um palco para continuar seguindo em frente com suas interações.
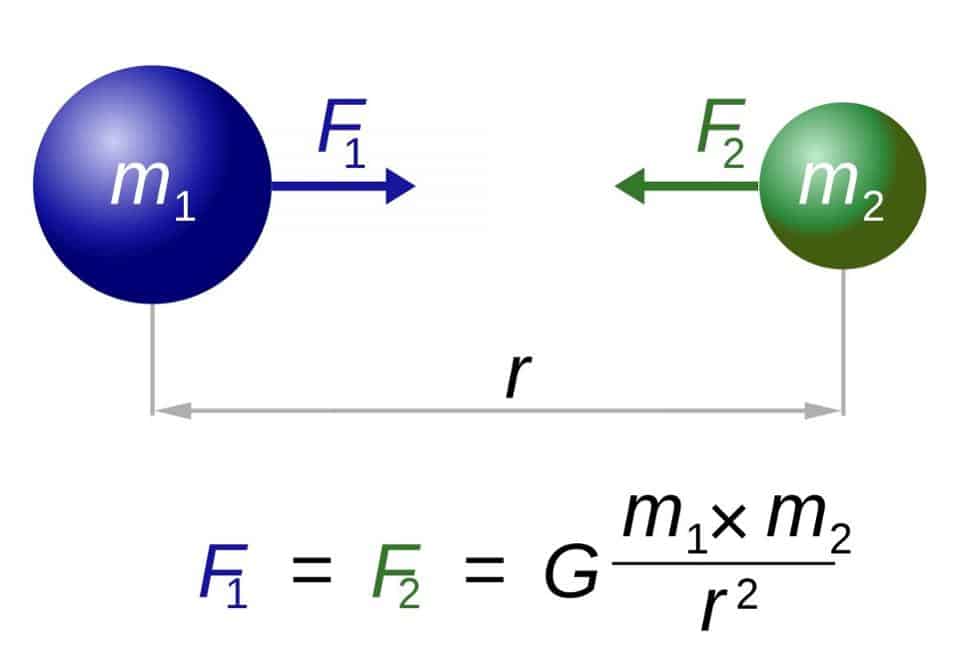
No universo de Newton, esse palco era plano, vazio e de espaço absoluto. O espaço em si era uma entidade fixa, como uma grande grade cartesiana: uma estrutura 3D com eixo x, y e z. O tempo sempre passava ao mesmo ritmo, e era absoluto também. Para qualquer observador, partícula, onda ou quantum em qualquer lugar, eles devem experimentar o espaço e o tempo exatamente iguais uns aos outros. Mas, no final do século XIX, ficou claro que a concepção de Newton era falha. As partículas que se movem próximas à velocidade da luz experimentam o tempo (se dilata) e o espaço (se contrai) de forma diferente em comparação com uma partícula que está se movendo lentamente, ou que está em repouso. A energia ou o momentum de uma partícula era, de repente, dependente da estrutura, significando que o espaço e o tempo não eram entidades absolutas; a forma como se experimenta o universo dependia de seu movimento através dele.
Créditos: John D. Norton.
Foi aí que surgiu a noção da teoria da relatividade especial de Einstein: algumas coisas eram invariantes, como a massa de uma partícula em repouso ou à velocidade da luz, mas outras variam conforme o modo como você se move pelo espaço e tempo. Em 1907, o antigo professor de Einstein, Hermann Minkowski, fez uma descoberta brilhante: mostrou que você poderia conceber o espaço e o tempo em uma única formulação. De uma só vez, ele desenvolveu o formalismo do espaço-tempo. Isso forneceu um palco para as partículas que se movem através do universo (relativo uma a outro) e interagem umas com as outras, mas não incluía a gravidade. O espaço-tempo que ele desenvolveu – ainda hoje conhecido como o espaço de Minkowski – descreve toda a relatividade especial, e também fornece o pano de fundo para a grande maioria dos cálculos da teoria quântica que fazemos.

Créditos: SLAN National Accelerator Laboratory.
Se não houvesse tal coisa como a força gravitacional, o espaço-tempo de Minkowski faria tudo o que precisávamos. O espaço-tempo seria simples, não curvo, e simplesmente forneceria um palco para que a matéria pudesse se mover e interagir. A única maneira de acelerar seria através de uma interação com outra partícula. Mas, no nosso universo, temos a força gravitacional, e foi o princípio de equivalência de Einstein que nos disse que, desde que você não consiga ver o que está acelerando você, a gravitação tratará você como qualquer outra aceleração.
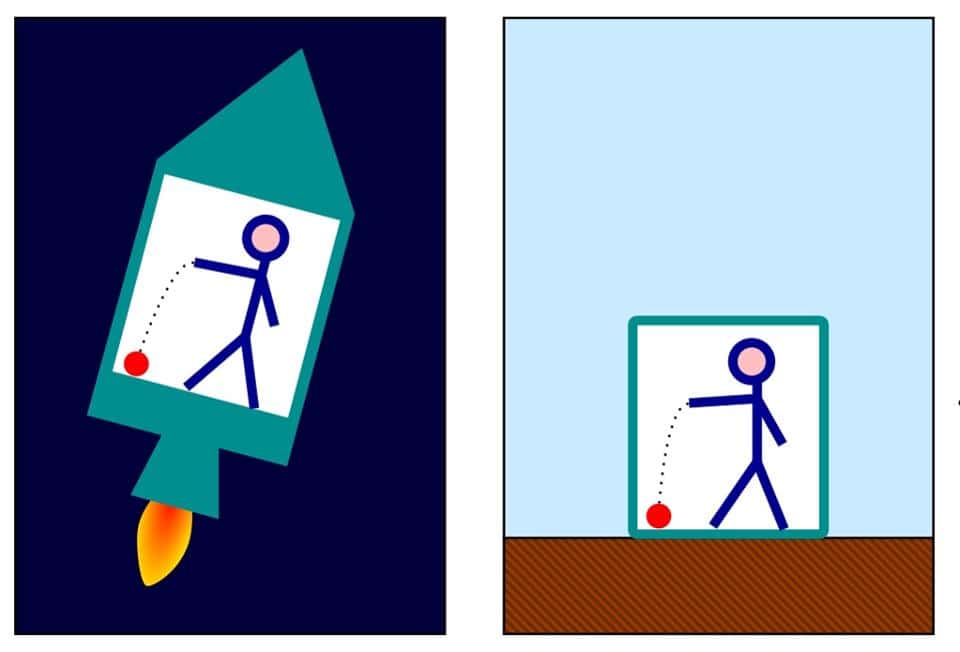
Créditos: Markus Poessel.
Foi essa revelação, e o desenvolvimento para vincular isso, matematicamente, ao conceito de espaço-tempo de Minkowski que levou à relatividade geral. A principal diferença entre o espaço de Minkowski da relatividade especial e o espaço curvo que aparece na relatividade geral é o formalismo matemático conhecido como Tensor Métrico, às vezes chamados de Tensor Métrico de Einstein, ou a Métrica de Riemann. Riemann era um matemático puro no século XIX (e um ex-aluno de Gauss, talvez o maior matemático de todos eles), e ele deu um formalismo para qualquer campo, linhas, arcos, distâncias, etc. que podem existir e ser bem definidos em um espaço arbitrariamente curvo de qualquer número de dimensões. Levou Einstein (e vários colaboradores) quase uma década para lidar com as complexidades da matemática, mas tudo foi dito e feito, tivemos, então, a relatividade geral: uma teoria que descreve nosso universo de três dimensões de espaço e uma de tempo, onde a gravitação existe.

Créditos: T. Pyle.
Conceitualmente, o Tensor Métrico define como o espaço-tempo, em si, é curvo. Sua curvatura depende da matéria, energia e tensões presentes dentro dele; o conteúdo de seu universo define a sua curvatura espacial no espaço-tempo. Pela mesma razão, a maneira que seu universo é curvo revela como a matéria e a energia vão se mover através dele. Gostamos de pensar que um objeto em movimento continuará em movimento: a primeira lei de Newton. Conceituamos isso como uma linha reta, mas o espaço curvo nos mostra que, em vez disso, um objeto em movimento que continua em movimento segue uma geodésica, que é uma linha particularmente curva que corresponde a um movimento não acelerado. Ironicamente, é uma geodésica, não necessariamente uma linha reta, que é a menor distância entre dois pontos. Isso aparece em escalas cósmicas, onde o espaço-tempo curvo, a partir da presença de massas extraordinárias, pode curvar a luz de fundo por trás dele, às vezes em múltiplas imagens.
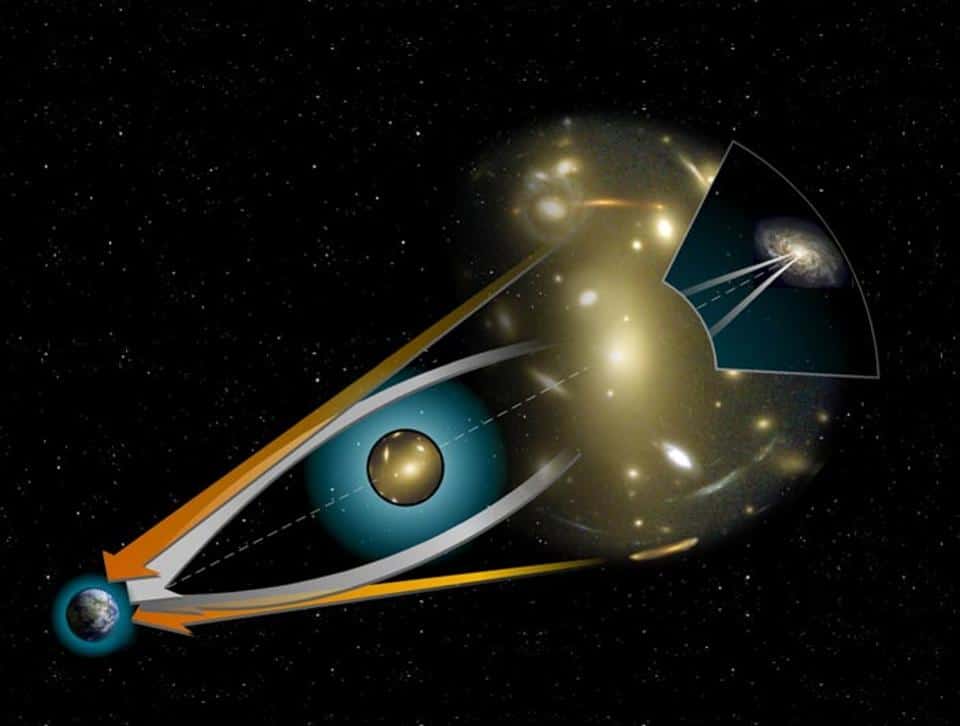
Créditos: NASA.
Fisicamente, há um número de partes diferentes que contribuem para o Tensor Métrico na relatividade geral. Pensamos na gravidade como devido às massas: os locais e as magnitudes de diferentes massas determinam a força gravitacional. Na relatividade geral, isso corresponde à densidade de massa e ainda contribui, mas é apenas um dos 16 componentes do Tensor Métrico! Há também componentes de pressão (como a pressão de radiação, pressão de vácuo ou pressões criadas por partículas de movimento rápido) que contribuem, que são os três contribuintes adicionais (uma para cada uma das três direções espaciais) para o tensor métrico. E, finalmente, há seis outros componentes que nos dizem como os volumes mudam e deformam na presença de massas e forças de maré, juntamente com a forma como o corpo em movimento é distorcido por essas forças. Isso se aplica a tudo, desde um planeta como a Terra até uma estrela de nêutrons a uma onda maciça que se move através do espaço: radiação gravitacional.

Créditos: ESO.
Você deve ter notado que 1 + 3 + 6 ≠ 16, mas 10, e se você notou, que ótima visão! O tensor métrico pode ser uma entidade 4 x 4, mas é simétrico, o que significa que existem quatro componentes “diagonais” (a densidade e os componentes de pressão) e seis fora da diagonal (os componentes de volume/deformação) que são independentes; os outros seis componentes fora da diagonal são determinados unicamente pela simetria. A métrica nos diz a relação entre toda a matéria/energia no universo e a curvatura do espaço-tempo em si. Na verdade, o poder único da relatividade geral nos diz que se você soubesse o que toda a matéria/energia do universo era e o que ela estava fazendo em qualquer instante, você poderia determinar toda a história evolutiva do universo – passado, presente e futuro – para toda a eternidade.
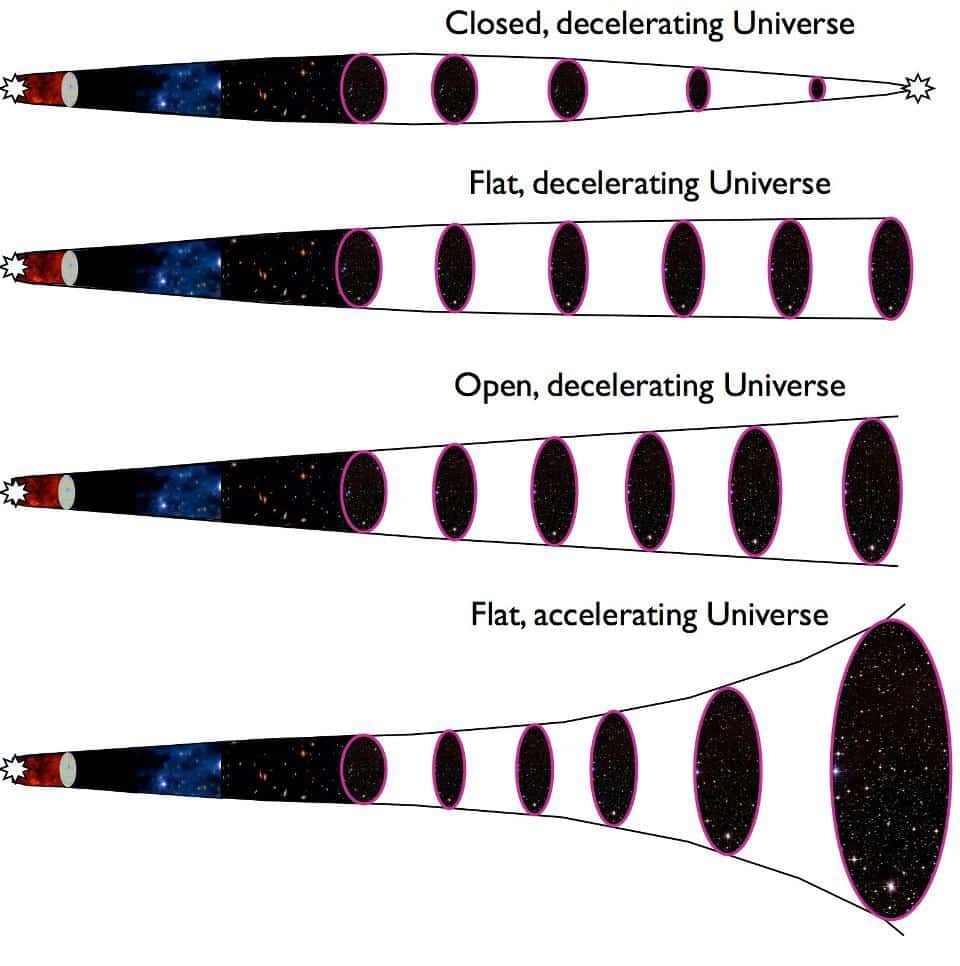
Créditos: Ethan Siegel.
É assim que meu subcampo de física teórica, a cosmologia, começou! A descoberta do universo em expansão, o surgimento do Big Bang e a dominação da energia escura que levará a um frio e vazio destino são todos apenas compreensíveis no contexto da relatividade geral, e isso significa entender essa relação chave: entre matéria/energia e espaço-tempo. O universo é uma peça de teatro, que se desenrola sempre que uma partícula interage com outra, e o espaço-tempo é o palco no qual tudo isso ocorre. Mas qual é a coisa mais contra-intuitiva que você deve ter em mente? O palco não é um cenário constante para todos, mas também evolui junto com o próprio universo.





